בחלק הקודם הצגנו את בעיית המדידה המתעוררת בפירוש המסורתי של תורת הקוונטים: מערכות פיזיקליות מתנהגות רוב הזמן לפי משוואת שרדינגר, ונמצאות בסופרפוזיציה של מצבים, וסופרפוזיציה היא מושג מתמטי ששונה לחלוטין ממה שאנו מכירים בטבע. מדידות, לעומת זאת, כרוכות בקריסה, תהליך שמביא את המערכת הפיזיקלית למצב שאנו מכירים, אבל אינו מתיישב עם משוואת שרדינגר, ולא ברור כיצד אפשר בכלל להגדיר אילו תהליכים פיזיקליים הם "מדידה" ואילו לא. ראינו את הפתרון של ויגנר, ואת זה של GRW. בחלק זה נבחן פתרונות אחרים.
דיוויד בוהם: בכל זאת, משתנה חבוי
במאמר מ-1952, "הצעת פירוש לתורת הקוונטים במונחים של 'משתנים חבויים"', ניסח דיוויד בוהם תיאוריה מוצלחת ביותר של משתנים חבויים, שאם היא נכונה, היא פותרת (בין השאר) את בעיית המדידה.
רגע רגע, מה זאת אומרת "אם היא נכונה"? הרי ג'ון סטיוארט בל הוכיח ב-1964, כפי שראינו בחלק ב', שלא תיתכן תיאוריה של משתנים חבויים! הפלא ופלא, לא רק שהתיאוריה של בוהם עומדת באתגר של בל, אלא שבל היה גם במשך כמה עשורים, עד מותו לאחרונה, חסיד מושבע שלה, ודאג במו־ידיו לקדם אותה אל תודעת עולם הפיזיקה, לאחר שנים רבות של כמעט־שכחה. אגב, כבר ב-1927, בתקופת הגיבוש הראשוני של תורת הקוונטים, הציע לואי דה־ברויי את הרעיון שביסוד התיאוריה של בוהם - אך הוא זנח את הרעיון מהר מדי, והשאיר לבוהם לפתח אותו באופן יסודי יותר.
מה אומרת התיאוריה של בוהם? ראשית, היא קובעת שחלקיקים לא נמצאים בסופרפוזיציה של מקומות: לכל חלקיק יש מקום מוגדר היטב. למעשה, המקום הזה הוא המשתנה החבוי, שקובע את תוצאתה של כל מדידה שנעשה לחלקיק. שנית, היא מאמצת את פונקציית הגל של תורת הקוונטים, אבל נותנת לה תפקיד אחר: בתורת הקוונטים פונקציית הגל רק מתארת את מצב החלקיק, ואת הידע שיכול להיות לנו עליו. אצל בוהם, יש לפונקציית הגל קיום עצמאי במרחב, והיא מניעה את החלקיק. בהינתן מקומו של החלקיק, ופונקציית הגל שלו, אז ניתן לחשב במדויק את מהירותו (באמצעות משוואה מסוימת). כך ניתן לחשב את מיקומו ברגע הבא. כזכור אנו יודעים לחשב גם את פונקציית הגל שלו ברגע הבא (בעזרת משוואת שרדינגר) – וכך ניתן לחזור על החישוב, ולבצע אותו עבור כל רגע עתידי. כלומר, ניתן לחשב במדויק את המסלול של החלקיק.
אבל אצל בוהם התנאים הללו נשארים היפותטיים: מסיבות שלא ניגע בהן כאן, התיאוריה שוללת מאיתנו כל דרך לדעת את מיקומו המדויק של החלקיק. המשתנה החבוי הוא באמת חבוי. כל מה שאנו יכולים לדעת הוא פונקציית הגל של החלקיק. אבל יש קשר בין השניים: כהנחה נוספת של התיאוריה, פונקציית הגל קובעת את ההסתברות של החלקיק להיות בכל נקודה במרחב: ההסתברות היא הגודל של פונקצית הגל באותה נקודה, בריבוע (בדומה לכלל בורן בתורת הקוונטים הקלאסית). המתמטיקה של התיאוריה מבטיחה שההנחה הזו נשמרת לאורך המסלול: אם בתחילת הניסוי ההסתברות להימצאותו של החלקיק בכל נקודה היא הריבוע של פונקציית הגל, ואנו עוקבים אחר המשוואות לתנועתו של החלקיק ולשינוי בפונקציית הגל, נקבל שגם בכל רגע עתידי ההסתברות למקום של החלקיק תהיה הריבוע של פונקציית הגל. לפיכך, מספיק להניח שההנחה התקיימה "ברגע בריאת העולם", ואנו מקבלים שהיא נכונה תמיד.
כאשר אנו מודדים לחלקיק גודל שאינו מקום, על־פי בוהם בעצם איננו מודדים שום תכונה אמיתית שלו: המקום המדויק שלו הוא מה שיקבע את תוצאת המדידה. למשל, ניסוי 1 (שטרן־גרלאך): לפני השדה המגנטי, פונקציית הגל היא כזו שהחלקיק נמצא, בהסתברות גבוהה מאוד, היכן שהוא במעגל קטן (האזור המרכזי של עקומת הפעמון המתארת את מיקומו):
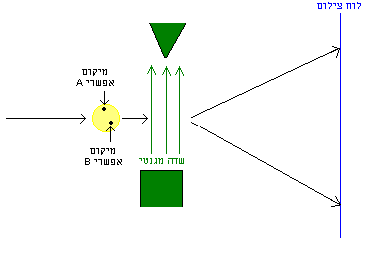
ואם החלקיק נמצא בחצי העליון של המעגל (למשל, בנקודה A), אז הוא יצא למעלה מהשדה; אם בחצי התחתון (למשל, נקודה B), אז הוא יצא למטה. (למעשה, אפשר היה לעטוף בציור את כל החיצים של המסלולים "בענן צהוב": בכל שלב בהמשך איננו יודעים את מקומו המדויק של האלקטרון, אלא רק הסתברות למצוא אותו בנקודות שונות בתחום מסוים, שבו יש ערך לפונקציית הגל. המסלולים המדויקים האפשריים אינם בהכרח קוים ישרים).
מה אם כיוון השדה היה הפוך ב-180 מעלות (מינוס-x)? פונקציית הגל של האלקטרון לפני השדה לא היתה שונה. ומכיוון שמסלולו של האלקטרון תלוי רק בפונקציית הגל ובמיקומו ההתחלתי, הרי שעדיין אם הוא היה ממוקם בחצי העליון הוא היה סוטה מעלה; אלא שהפעם היינו אומרים שהספין מינוס-x שלו הוא 'מעלה', כלומר הספין-x שלו הוא 'מטה'! כשאנו אומרים שמדדנו לאלקטרון ספין-x 'מעלה', או 'מטה', בעצם לא מדדנו שום תכונה אמיתית של האלקטרון; מדדנו יחס מסוים בין מצבו לבין מערך הניסוי שלנו. תכונת הספין היא, אצל בוהם, "תכונה הקשרית" (קונטקסטואלית) - היא קשורה קשר הדוק למערך הניסוי, ובעצם אינה "תכונה" במובן המקובל - וכמוה כל התכונות של חלקיקים, פרט למקום. אם ניזכר בתיאורית הקריסה של GRW מהחלק הקודם, גם שם המקום הוא תכונה "אמיתית" יותר מ"תכונות" אחרות, והוא קובע אותן, אך מסיבות אחרות.
ניזכר בניסוי 2 מחלק א'. שם אנו מעבירים את האלקטרונים שיצאו מעלה מהשדה המגנטי דרך שדה מגנטי נוסף באותו כיוון, וכולם יוצאים מעלה (מה שגרם לנו לומר שנראה כי הספין הוא תכונה של האלקטרון). כזכור, על פי תורת הקוונטים הקלאסית, המעבר בשדה הראשון (בהיותו מדידה) גרם לפונקצית הגל לקרוס ל'מעלה', ולכן לשדה השני מגיעים אלקטרונים עם ספין 'מעלה'. על פי בוהם, פונקציית הגל של האלקטרון היא עדיין בסופרפוזיציה של מעלה־מטה; אבל אם האלקטרון נע במסלול העליון, רק רכיב ה'מעלה' בפונקצית הגל משפיע על מהירותו (ומכאן, על מסלולו). ההפרדה בין המסלולים גורמת לרכיב אחד להיות "לא רלוונטי", ואפשר לקרוא לכך "קריסה־למעשה". מבחינת התוצאות התצפיתיות שלה, היא נראית כמו הקריסה של תורת הקוונטים. אך מבחינת המכניזם הפנימי בתיאוריה, זוהי התפתחות נורמלית בזמן על־פי המשוואות, ולא תהליך מסתורי שמנוגד למשוואת התנועה הרגילה (כמו הקריסה בתורת הקוונטים). וכך נפתרת בעיית המדידה.
בניסוי EPR, כזכור, אנו שולחים זוג חלקיקים בכיוונים מנוגדים, מודדים לשניהם בשתי נקודות רחוקות ספין באותו כיוון, ומקבלים תוצאה זהה. איך מטפלת בכך התיאוריה של בוהם? כזכור, בתורת הקוונטים שני החלקיקים מהווים מערכת אחת, ומתארת אותם פונקצית גל אחת. כך גם אצל בוהם. אמרנו שבתורת בוהם, המהירות של חלקיק נקבעת על־ידי פונקציית הגל שלו ומיקומו. כאשר המערכת מורכבת מיותר מחלקיק אחד, המהירות של החלקיק נקבעת על ידי פונקציית הגל של המערכת, והמיקום של כל החלקיקים בה. מה שקורה לחלקיק אחד משפיע ישירות (באופן שמתבטא במשוואות) על החלקיק השני. וההשפעה היא כזו שאם מדדנו בצד ימין ספין, והאלקטרון סטה מעלה, אז רכיב ה'מטה' בפונקציית הגל יפסיק להשפיע גם על האלקטרון שמדדנו, וגם על האלקטרון השני. והשינוי הזה יתרחש מיידית, ללא תלות במרחק. והנה אנו מגלים כיצד עומדת התורה באי־שוויון בל.
אמרנו שאי־שוויון בל שולל משתנים חבויים. אבל זה לא היה מדויק. נכון יותר לומר שבל שלל תורות משתנים חבויים לוקאליות. ההסבר הנוח של ניסוי EPR בעזרת משתנים חבויים היה לוקאלי: כשהחלקיקים יוצאים מהמקור המשותף, יש בהם מידע שיקבע את תוצאות הניסוי העתידי, ויעשה זאת ללא השפעה ממרחק. אפשרות כזו נשללה על־ידי בל. תורת בוהם היא לא לוקאלית, וטוענת להשפעה מיידית ממרחק. היא לא נותנת את ההסבר האינטואיטיבי־הנוח ל-EPR, ולכן היא גם לא נסתרת על־ידי בל.
אז מה עדיף, תורת הקוונטים הקלאסית או תורת בוהם?
תורת בוהם, בניגוד לתורת הקוונטים, היא דטרמיניסטית: התוצאה של ניסויים נקבעת מראש, על־פי מיקומם המדויק של החלקיקים. אבל את המיקום הזה לא ניתן לדעת, אלא הסתברותית על־פי פונקציית הגל. בתורת הקוונטים יש לנו אי־ודאות מהותית, כאשר מיקומו של החלקיק (שנמצא בסופרפוזיציה) אינו מוגדר, ולא ניתן לומר שהוא נמצא בנקודה זו או באחרת. בתורת בוהם מחליפה אותה אי־ודאות אפיסטמית, כלומר שנובעת מחוסר ידע. יש לחלקיק מקום מוגדר, ורק אנחנו לא יודעים אותו. מבחינה ניסיונית אין הבדל, וזהו מאפיין קריטי של תורת בוהם: אין ניסוי, ולו תיאורטי, שיבחין בינה לבין תורת הקוונטים הקלאסית - בניגוד, למשל, לתיאוריית GRW. העדפתה או דחייתה נתונות לשיקולים מטאפיזיים־פילוסופיים. הבה נראה מה עומד על הכף:
למרות שאין ניסוי שיבחין ביניהן, לא יהיה זה מדויק לומר שהתיאוריות שקולות מבחינה ניסיונית. זאת בגלל שיש ניסויים, בינתיים תיאורטיים, שלא ברור בכלל מה אומרת עליהם תורת הקוונטים, ואילו אצל בוהם יש סיפור ברור - למשל החתול של שרדינגר.
שתי התיאוריות הן אי־לוקאליות, אבל יש לאי־הלוקאליות הזו טעם אחר קצת. בתורת הקוונטים הקלאסית הקריסה היא בו־זמנית בכל מקום שבו פונקציית הגל רלוונטית, אבל ממילא התורה לא אומרת הרבה על מהותה של הקריסה הזו. כך שההיבט הבעייתי הוא בתחום שממילא הוא מעורפל משהו. אצל בוהם השינוי הלא־לוקאלי בפונקציית הגל הוא תהליך פיזיקלי מוגדר היטב, ואפשר ממש לראות בו הפעלת כוח על חלקיקים כך שמסלולם ישתנה. אפשר לומר כי בתורת בוהם האי־לוקאליות היא מפורשת וחד־משמעית יותר, כך שאם יש לנו בעיה עם אי־לוקאליות, הבעיה חריפה יותר בתורת בוהם. עד 1964 אפשר היה אולי לראות בכך חסרון - אבל הרי אי־שוויון בל הראה לנו שהמציאות היא לא־לוקאלית. לכן, אין כאן בעיה של תורת בוהם דווקא.
תורת הקוונטים הקלאסית היא אקראית, ומכילה אי־ודאות מהותית, לעומת תורת בוהם, שהיא דטרמיניסטית והאי־וודאות בה היא רק חוסר ידע. פיזיקאים רבים, הבולט שבהם איינשטיין, רואים באקראיות רעה חולה - ממש לא יתכן, לשיטתם, שהעולם באמת אקראי ביסודו. תורת בוהם היא בדיוק מה שהם חיפשו. אבל קשה לחשוב על נימוק מטאפיזי משכנע, מדוע העולם יהיה דווקא דטרמיניסטי ולא אקראי. אולי זה סתם קיבעון מחשבתי מיותר, אמונה טפלה ותו לא?
ההישג הגדול של תורת בוהם, בעיני, הוא פתרון אלגנטי של בעיית המדידה. היא משלימה את תורת הקוונטים הקלאסית, היכן שזו אינה שלמה. אבל היא דורשת קבלה של הנחות מבלי שיש לנו כל עדות ניסיונית לנכונותן, ומבלי שתהיה לנו עדות כזו אי־פעם. מידת האהדה שלנו לתורה היא אולי עניין של טעם - מכל מקום, חשוב לזכור כי האפשרות שהציג בוהם קיימת.
בעיות עם תורת היחסות
בדיון על אי־שוויון בל בחלק ב' אמרנו שהקריסה בתורת הקוונטים המסורתית אינה מתיישבת היטב עם תורת היחסות, מכיוון שהיא מתרחשת בו־זמנית במקומות מרוחקים. בעיה זו לא נפתרת על־ידי תורת GRW, ולא על־ידי תורת בוהם. לתורת הקוונטים המסורתית יש הרחבות שבאות ליישב אותה עם תורת היחסות. עקרונית אולי ניתן יהיה לעשות זאת גם לתיאוריות של בוהם ושל GRW, אולם עד כה נסיונות כאלו נתקלו בקשיים גדולים. לכאורה אין מנוס מזה, בעקבות EPR ובל. אבל יש תיאוריות שבכל זאת מנסות להיחלץ מהמלכודת, באמצעים רדיקליים באמת: לוותר בכלל על קריסה, ולטעון שיש סופרפוזיציה גם היכן שלכאורה ברור שאין.
תיאוריית העולמות המרובים ואחיותיה
הניסיונות בכיוון החלו ב-1957, במאמר של יו אברט (Hugh Everett) ה-III, "פירוש 'המצב היחסי' למכניקת הקוונטים". גרעין הרעיון שלו הוא שאין קריסה בכלל: בניסוי 1, למשל, שתי התוצאות נכונות באותה מידה: האלקטרון עבר בשדה מגנטי, נכנס לסופרפוזיציה של שני המסלולים, שתי נקודות על המסך נדלקו בסופרפוזיציה. גם המוח של הצופה, ואיתו התודעה, נכנסים לסופרפוזיציה, בין המצב המתאים ל"ראה נקודה A נדלקת" לזה המתאים ל"ראה נקודה B נדלקת". אלא שאצל אברט, כל תוצאה שהצופה רואה מוגדרת רק ביחס לרכיב מסוים בסופרפוזיציה, הכוללת את מצב האלקטרון. ביחס לרכיב בו האלקטרון נע למעלה, הצופה ראה A; ביחס לרכיב בו האלקטרון נע למטה, הצופה ראה B. לומר כעובדה "הצופה ראה A" לא יהיה תיאור נכון של העולם.
המצב היחסי של הצופה כולל זיכרון: נניח שמדדנו ספין לשני אלקטרונים. במחשבה המסורתית, יש ארבע תוצאות אפשריות: הראשון 'מעלה', השני 'מטה'; הראשון 'מטה', השני 'מעלה'; שניהם 'מעלה'; שניהם 'מטה'. אצל אברט יש תוצאה אחת: העולם (החלקיקים והצופה) לאחר המדידה השניה מתואר על־ידי סופרפוזיציה של ארבעה רכיבים. יש רכיב אחד בו הצופה ראה נקודה A נדלקת, ביחס למדידה הקודמת שבה הוא ראה - או ליתר דיוק, ביחס לזיכרון שלו שהוא ראה A קודם (וביחס למצבים המתאימים של שני האלקטרונים); רכיב אחר בו הצופה ראה A ביחס לתצפית קודמת של B; וכן הלאה. כל מדידה יוצרת עוד ועוד מצבים יחסיים. לאחר 10 מדידות יהיו שתיים בחזקת 10 רכיבים בסופרפוזיציה, או מצבים יחסיים. הריבוי הזה הוא בגלל שאין קריסה: בתורת הקוונטים המסורתית, תמיד יש (בסדרת ניסויי ספין) לכל היותר סופרפוזיציה של שני רכיבים, ואז קריסה לאחד.
אברט צריך את ההתייחסות הזו לזיכרון של מדידות קודמות כדי להסביר למה אנו רואים סטטיסטיקות כאלו ואחרות של תוצאות בסדרות ניסויים. כפי שנראה מיד, זה לא ממש מצליח לו. אבל קשה לראות זאת אצל אברט, כי ממילא לא ברור עד הסוף מה הוא אומר: הוא לא ניסח במפורש התחייבות מטאפיזית על מה שקורה אצל הצופה, ולמה בדיוק הצופה חושב שהוא רואה תוצאה אחת מוגדרת היטב. הפירוש שלו לתורת הקוונטים דורש בעצמו פירוש; למעשה, הוצעו פירושים רבים, ונסקור כאן כמה מהם. המשותף לכולם הוא היתרון האחד הגדול שאברט רוצה להפיק מהתיאוריה שלו: ויתור על הצורך בקריסה.
הפירוש המפורסם ביותר הוא זה של ברייס דוויט (DeWitt), שהוצג ב-1970. אצל אברט, מבחין דוויט, אין תקשורת ואינטראקציה בין המצבים היחסיים השונים של הצופה: התודעה של הצופה מתחלקת למין סטים של זיכרונות, שכל אחד מהם לחלוטין לא מודע לאחרים. אבל אין גם השפעה פיזיקלית בין המצבים השונים: כל אחד מהם מתפתח באופן עצמאי, כאילו היה עולם נפרד. אז אולי הם באמת עולמות נפרדים? זה מה שמציע דוויט: בכל מדידה שיש לה שתי תוצאות אפשריות, העולם מתפצל לשניים: עולם אחד שבו לאלקטרון נמדד ספין 'מעלה', ועולם שני שבו לאלקטרון נמדד ספין 'מטה'. לצופה שלנו נהיים מיד שני עותקים, כמעט זהים, פרט לכך שאחד מהם ראה A והשני B. מכיוון שמאז בריאת היקום היו המוני אינטראקציות קוונטיות, הרי שהיקום מורכב מאינספור עולמות, שעוד הולכים ומתרבים. ברובם אנו לא קיימים בכלל. זהו "פירוש העולמות המרובים".
האינטואיציה המקובלת מתקוממת נגד ראייה כזו, והדבר מוצא ביטוי גם בטיעון פילוסופי נגד התיאוריה, לפיו היא מציעה "אקסטרווגנזה אונטולוגית" - ריבוי שערורייתי של "היש". אבל יש לו גם בעיות בתחום הפיזיקה היבשה. הקשה שבהן היא שהוא לא מצליח לתת הסבר לתוצאות סטטיסטיות. אנו יודעים על מערך ניסוי שבו הסיכוי למדוד ספין 'מעלה' הוא חצי, והסיכוי לספין 'מטה' הוא חצי. ונניח שעשינו מאה מדידות. אצל דוויט, יש לנו כעת שתיים בחזקת מאה עולמות, ובכל אחד מהם התקבל יחס שונה של תוצאות (קיים אפילו עולם אחד שבו כל המאה יצאו 'מעלה'). כיצד ניתן לדבר על "יחס חצי־חצי"?
קל להראות מתמטית שברוב העולמות היחס יהיה קרוב לחצי־חצי, ובאופן יותר מדויק, השכיחות היחסית של העולמות מתאימה להסתברות המבוקשת. ואולי אפשר (אם כי עדיין לא קל) להפיק מזה דיבור על הסתברות כפי שאנו רואים אותה. עוד עובדה מתמטית שחסידי התיאוריה מתלהבים ממנה (היא הוצגה כבר במאמר של אברט) היא שלאחר אינסוף מדידות, היחס בין התוצאות שואף לחצי־חצי בהכרח, בכל אינסוף העולמות. אבל לא ברור מה זה עוזר כשמדובר במספר סופי של מדידות, והרי בפועל מעולם לא ביצענו אינסוף מדידות.
יתרה מכך, דוויט נשאר חסר אונים, כך נראה, אם משנים את הניסוי כך שהיחס שונה מחצי־חצי (למשל, 1/4-3/4, וראינו כיצד ניתן לעשות זאת). השכיחות היחסית של העולמות על פי דוויט נשארת בדיוק כמו בניסוי הקודם, ולכן, אם הוא מצליח להפיק מכך הסבר סטטיסטי, ההסבר לא יהיה תואם לתוצאות הניסוי.
הפיזיקאי הישראלי לב ויידמן מציע גרסה שמתקנת את הבעיה הזו. ויידמן פשוט מכניס את ההסתברות כהנחה נוספת בתיאוריה: לא כל העולמות נולדו שווים. אם בניסוי מסוים ההסתברות (בפרשנות המסורתית) היא 3/4 'מעלה' - 1/4 'מטה', אז מבין שני העולמות שיווצרו, לזה שבו המדידה היא 'מעלה' תהיה "מידת קיום" גדולה יותר - ההסתברות שלו תהיה גדולה פי 3 משל השני. לא לגמרי ברור מה זה אומר, כלומר איך ליישב זאת עם מושגים מקובלים של הסתברות.
לפירושים של דוויט וויידמן משותפת בעיית "הבסיס המועדף": המודל המתמטי של תורת הקוונטים מאפשר לרשום פונקציית גל מסוימת במספר דרכים, למעשה אינסוף דרכים, שכולן שקולות מתמטית. בחלק מהדרכים יהיה מספר שונה של רכיבים בסופרפוזיציה. ראינו זאת בספינים: אמרנו כי ספין-x 'מעלה' הוא סופרפוזיציה של ספין-y 'מעלה' וספין-y 'מטה'; פירוש הדבר הוא שתי דרכים שונות לרשום את אותו המצב. קוראים לזה בסיסים שונים. בפירוש של עולמות מרובים יש לכך לפתע השלכה על הפיזיקה: שני התיאורים נותנים לנו מספר שונה של עולמות, ולכן נבדלים מהותית. צריך להיות, אם כן, בסיס אחד שהוא הנכון לתיאור העולם, ותורת הקוונטים לא רומזת על כך. יש נסיונות מבטיחים למציאת נימוקים פיזיקליים להעדפת בסיס מסוים, אך זו עדיין בעיה לא פתורה.
בגרסה שהציע דיוויד דויטש ב-1985 יש מלכתחילה אינסוף עולמות, שמתפצלים בכל ניסוי בהתאם ליחס ההסתברות המקובל; בכל אחד מהענפים עדיין יש אינסוף עולמות, כך שאין מניעה שההתפצלות תימשך ללא הרף. לגישה כזו יש אולי יותר סיכוי לטפל בהסתברויות ולא להזדקק לבסיס מועדף.
להעביר את הבעיה אל התודעה
כיוון מעניין הוא לשלב בין אברט לוויגנר, בו נתקלנו בחלק ג'. ויגנר טען שהתודעה היא הגורמת לקריסה בעולם הפיזיקלי. אברט טוען שאין קריסה. אולי האמת היא שבעולם הפיזיקלי אין קריסה, והיקום כולו נמצא בסופרפוזיציה רבתי; אבל התודעה, או הנפש, בוחרת ללא הרף רכיב מסוים (מבלי שהבחירה תשפיע על פונקצית הגל הפיזיקלית). ה"בחירה" של התודעה ברכיב מסוים היא אקראית, ונעשית בהסתברות הזכורה לנו מכלל בורן - הגודל של פונקצית הגל בריבוע.
קיבלנו את מה שרצינו: בלי קריסה פיזיקלית, בלי בעיות קונצפטואליות הכרוכות בריבוי של הצופה, ובלי בעיות בהסבר הסטטיסטיקה. אנו מחויבים מייד, כמובן, לדואליזם בבעיית הגוף־נפש: בתיאוריה זו ייתכנו שני אנשים שהמצב הפיזיקלי של מוחם זהה לחלוטין, ובכל זאת מצבם התודעתי שונה: אחד ראה (או נדמה לו שראה) ספין 'מעלה', והשני ספין 'מטה' - רק בגלל שתודעתם בחרה אקראית רכיבים שונים. יש שרואים בכך בעיה, אבל לא כולם, שהרי עוד לפני תורת הקוונטים לא היה ברור שהנפש היא באמת פיזיקלית.
בחלק ג' טענו כנגד הפרשנות של ויגנר, שהיא מדברת על תודעה ולא אומרת מהי תודעה ומה לא. לכאורה, גם כאן יש לנו בעיה כזו. אבל לא כך: אצל ויגנר, יש לתודעה תפקיד פיזיקלי - היא מחוללת את הקריסה. התודעה של הסטודנט שראה את המחוג משנה את המצב הפיזיקלי בעולם; אם היה על השולחן חגב שהסתכל על המחוג לפני הסטודנט, השאלה האם לחגב יש תודעה או לא, היא שאלה משמעותית. ומכיוון שויגנר לא נותן תשובה (ואין לו כלים לכך), התיאור שלו את העולם מעורפל לא פחות משל הפרשנות המסורתית (בעיית המדידה). לעומת זאת, בפרשנות שלנו כאן אין לתודעה השפעה על המציאות הפיזיקלית. אנו מדברים על התודעה רק כהסבר לדברים שאנו רואים בתודעתנו; השאלה האם לחגב יש תודעה לא צריכה לעניין אותנו, כל עוד איננו מתעניינים בפסיכולוגיה של חגבים.
אבל עכשיו יש לנו בעיה מסוג חדש. עכשיו מתברר שכצופים, אנו בכלל לא צופים אמינים: נדמה לנו שראינו נקודה A על המסך זוהרת, אבל זה דיווח שקרי של התודעה שלנו: בפועל זה לא מה שראינו (לפחות במישור הפיזיקלי של הראיה), כי ראינו את הנקודות A ו-B זוהרות בסופרפוזיציה. זה מסתבך עוד יותר בסיטואציה הבאה: נניח שעמי ותמי הם שני סטודנטים לפיזיקה, שביצעו מדידה והסתכלו שניהם על התוצאה, A או B. על פי התורה הזו, בהחלט יתכן שהתודעה של עמי ראתה (נדמה לעמי שהוא ראה) A, ושל תמי - B. אבל מה קורה אם תמי שואלת את עמי מה עמי ראה? יש לנו שתי דרכים לנתח זאת. האחת היא שהתודעה של עמי קובעת מה עמי יגיד. אבל אז עמי יגיד A, ותמי תבחין בסתירה לתודעתה שלה. במעבדה לרוב אין חילוקי דעות כאלו בין סטודנטים, לכן אפשרות זו נפסלת. הניתוח השני הוא שמה שעמי יגיד, פיזיקלית, לא תלוי בתודעה שלו, אלא נובע ישירות מהמצב הפיזיקלי של המוח שלו: כלומר, עמי יגיד A ויגיד B בסופרפוזיציה. אז אין בעיה: נזכור כי עמי ותמי (והחלקיק והמכשיר), כולל מה שעמי אמר (פיזיקלית), מתוארים על־ידי פונקציית גל אחת גדולה, עם שני רכיבים. אם התודעה של תמי בחרה לאחר המדידה ברכיב B, אז היא כבר "מחויבת" לכל הרכיב, והיא "תשמע" את התשובה "B" מתוך הסופרפוזיציה של התשובות. תמי לא תחשוב שיש סתירה.
הישג מעניין שקיבלנו כאן הוא פתרון של בעיית האי־לוקאליות. ההתפתחות הפיזיקלית היא כולה לוקאלית (ואי־שוויון בל אינו תופס, ברמה הפיזיקלית, כי כמובן התוצאות 'מעלה' ו'מטה' קיימות שתיהן, בסופרפוזיציה). התודעה של כל צופה בוחרת רכיב באופן עצמאי, ואין צורך להניח "השפעה מרחוק".
אבל יש גם תוצאה פחות נעימה: התודעות שלנו מנותקות מגופנו הפיזיקלי במידה כזו, שהגוף אדיש להן לחלוטין; כל מה שאנו חושבים על עצמנו הוא אשליה אחת גדולה. תמי שאלה את עמי, אבל אפשר לומר שהיא שמעה רק מה שהיא רצתה לשמוע, בלי קשר למה שעמי אמר. אם עמי ראה A ותמי B, תמי "תשמע" מעמי תשובה "B", אבל התשובה הזו לא תבוא מאישיות בעלת תודעה; היא תבוא מ"גולם חסר־תודעה" (mindless hulk), מונח שטבעו דיוויד אלברט ובארי לואר ב-1988.
אלברט ולואר פתרו זאת בעזרת פרשנות "התודעות המרובות" (many minds). בפרשנות זו העולם הפיזיקלי הוא אחד, דטרמיניסטי, ללא קריסות, ומכיל סופרפוזיציות; לכל מוח בו צמודות אינסוף תודעות. כל תודעה צמודה לערך מסוים מתוך הסופרפוזיציה של מצבי המוח - למעשה, לכל ערך של מדידה שאותו צופה מדד, יש אינסוף תודעות ש"ראו" את הערך הזה. היחס בין מספר התודעות שראו כל ערך הוא, איך לא, ריבוע הגודל של פונקציית הגל באותו ערך.
מה נאמר על הסיטואציה שתיארנו, שבה תמי שואלת את עמי מה ראה? כאן ברור שעמי יענה בסופרפוזיציה של "A" ו-"B", לא משנה מה אנו חושבים על השפעת התודעה על המוח: גם אם התודעה משפיעה על המוח, ממילא כל אחת מהתודעות תשפיע על הרכיב המתאים לה בסופרפוזיציה של המוח; ומכאן, שהרכיב שראה־פיזיקלית A גם יגיד A, והרכיב שראה־פיזיקלית B יגיד B. שוב, התודעות של תמי שראו A ישמעו A, והתודעות שראו B ישמעו B. אבל הפעם אכן יעמוד משהו - ליתר דיוק, מישהו - מאחורי התשובות של עמי שתמי קולטת. חצי מהתודעות של תמי, אלו שראו תוצאה B, גם שמעו "B" מעמי - והתשובה הזו באה אכן מתוך תודעה של עמי שראתה B.
קיבלנו, אם כן, תורה שאינה זקוקה לקריסה, על כל בעיותיה, שהיא לוקאלית לחלוטין, ושהתודעה בה היא אמינה, לפחות במובן מסוים (ניתן לומר שהיא מספרת את האמת, אם כי לא את כל האמת). מאידך, היא גורסת שהעולם הפיזיקלי הוא סופרפוזיציה אחת גדולה (ולכן תפיסתנו אותו היא אשליה), ובנוסף לכך מניחה פיצול אישיות אינסופי. הקורא מוזמן לחשוב האם ההישג שווה את המחיר.
סיכום
ג'ון סטיוארט בל היה, כאמור, חסיד נלהב של תורת בוהם. למעשה הוא אמר שבעיית המדידה נפתרה, והבעיה המושגית הקשה שנותרה בתורת הקוונטים היא ההשתלבות שלה עם תורת היחסות. התיאוריות ללא קריסה מנסות לחמוק מבעיה זו, אבל במחיר מטאפיזי שרבים יאמרו שהוא שערורייתי (כל גרסה של התיאוריה משלמת במקום אחר). בעיני גם ההצהרה הזו של בל היא אולי מוקדמת: יש משהו טורד מנוחה בעובדה שהפתרון של בוהם אינו ניתן לאישוש ניסיוני (או לפחות לא להבחנה ניסיונית מהפרשנות המסורתית) - וכך גם התיאוריות ללא קריסה. שיקולים פילוסופיים ממלאים כאן תפקיד לא פחות מהשיקולים הפיזיקליים, וההרפתקה האינטלקטואלית הזו לא נראית קרובה לקיצה.
קריאה נוספת
הספר Quantum Mechanics and Experience של דיוויד אלברט (1992) מומלץ בכל פה. הוא מטפל בערך באותם נושאים שטופלו בסדרת המאמרים, באופן מרתק, קריא ומדויק מבחינה פילוסופית. הוא משתמש ביותר מתמטיקה (אלגברה ליניארית), אך מסביר אותה לאט, ולכן לא מצריך ידע מתמטי מוקדם. השימוש בה מאפשר לו דיון מדויק יותר מכפי שהתאפשר כאן. למרבה הצער, הוא אזל בדפוס. אפשר לנסות לדוג אותו באינטרנט, או למצוא אותו בספריות אוניברסיטאיות.
ישנם מספר מאמרים רלוונטיים באנציקלופדיה הפילוסופית המקוונת של סטנפורד. רובם נכתבו על־ידי מומחים מובילים בתחום, והם עדכניים ומכילים קישורים למאמרים רלוונטיים אחרים. מאמר המבוא נותן הסבר מתמטי בערך ברמה של אלברט, אך בצורה חפוזה, ולכן יתאים יותר למי שכבר למד פעם אלגברה ליניארית ברמה אקדמית. שאר המאמרים מכילים מידה זו או אחרת של משוואות מתמטיות ומושגים פיזיקליים שמצריכים רקע מוקדם. מומלצים בכל־זאת אלו של לב ויידמן, על הגרסה שלו לתיאורית העולמות המרובים, ושל ג'אנקרלו גירארדי (ה-G ב-GRW) על תיאוריית הקריסה של GRW.
|
קישורים
מאמר המבוא למודל המתמטי של תורת הקוונטים
לב ויידמן, על הגרסה שלו לתיאוריית העולמות המרובים
ג'אנקרלו גירארדי על תיאוריית הקריסה של GRW
|









































 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות

