 |
"הפסנתר המושווה" - מה מושווה בו? סולמות, מרווחים וכוון כלים, מפיתגורס ועד ימינו.
|
|
| מוזיקה • יובל נוב • יום ד', 21/1/2004, 19:56 |
|
 |
|
| יוהן סבסטיאן באך (ציור מאת אליאס גוטליב האוסמן, 1748) |
|
בשנת 1717 הגיע לעיר קתן (Köthen) בגרמניה מוסיקאי צעיר בשם יוהן סבסטיאן באך. במהלך שש השנים ששימש כמוסיקאי החצר של ליאופולד, הנסיך המקומי, הספיק באך להתאלמן, להנשא מחדש ולהוליד שניים מתוך עשרים ילדיו, אבל גם להשלים את הכרך הראשון של "הפסנתר המושווה" (das Wohltemperiertes Klavier) - אוסף של עשרים וארבעה פרלודים ופוגות, הנמנה לדעת רבים על יצירות המופת המוסיקליות החשובות בכל הזמנים.
כפי ששם היצירה מרמז, באך חיבר אותה עבור כלי־מקלדת שכוונו בשיטה מסוימת - שיטה שנחשבה באותה התקופה למהפכנית. מדוע, בעצם, קיימת יותר משיטה אחת לכוון המקלדת? במאמר זה ננסה לענות על שאלה זו, ובעיקר לתאר את שיטת הכוון המקובלת כיום. בטרם נתחיל, התנצלות קלה: יריעת "האייל הקורא" היא צרה מכדי להכיל דיון ממצה בסוגיית הכוון, ולכן ההסברים שלהלן הם פשטניים, במידה מסוימת.
מהו צליל?
צלילים הם תנודות מחזוריות בלחץ האויר, בהן אנו מסוגלים לחוש באמצעות עור התוף שבאוזננו. אם נשרטט גרף של לחץ האויר כתלות בזמן בעת שאנו שומעים צליל, נקבל צורת "גל" החוזר על עצמו, כדוגמת השלושה שלהלן.
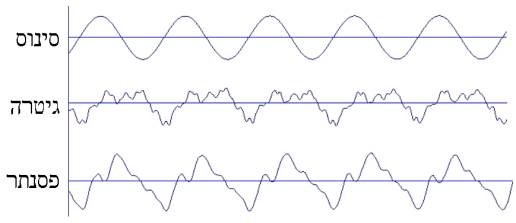
הגל העליון - הפשוט מבין השלושה - נוצר על ידי מחשב, וניתן לשמוע אותו בדוגמה 1. גל זה מתאים לפונקצייה מתמטית בסיסית הנקראת סינוס, ואולי בשל כך הוא נשמע "סינתטי" או "משעמם". לגלים הנוצרים על ידי כלי־נגינה אמיתיים יש צורה מורכבת בהרבה - הגל השני הוא של גיטרה (דוגמה 2), והשלישי, של פסנתר (דוגמה 3). המשותף לשלושת הגלים שלעיל הוא המחזוריות - שלושתם מורכבים מ"יחידה בסיסית" מסויימת החוזרת על עצמה שוב ושוב; הם נבדלים זה מזה רק בצורתה של אותה "יחידה בסיסית". הבדלי צורה אלה הם הגורם העיקרי (אך לא היחיד) המגדיר את גוון הצליל - בזכותם אנו מסוגלים להבחין, למשל, בין צליליהם של חצוצרה וכינור.
מספר המחזורים שגל משלים בשנייה נקרא התדירות שלו, והיחידה המשמשת למדידת תדירות נקראת הרץ. ככל שהתדירות גבוהה יותר, אורך ה"יחידה הבסיסית" קצר יותר, ואנחנו קוראים לצליל המתקבל "גבוה" יותר. שלושת הצלילים ששמענו לעיל היו בתדירות 440 הרץ, ומוסיקאים נתנו לצליל בתדירות זו את השם "לה"; מסיבות היסטוריות, נהוג לכוון כלי־נגינה ביחס אליו. כשהיא במיטבה, האוזן האנושית מסוגלת להבחין בצלילים שתדירויותיהם הן בין 20 ל- 20,000 הרץ. למרבה הצער, תחום זה מצטמצם משמעותית עם השנים, וגבולו העליון יורד לרוב מתחת ל- 10,000 הרץ לאחר גיל 55. לשם השוואה, תחום השמע של עכברים הוא 91,000 - 1,000 הרץ, ושל פילים, 12,000 - 16 הרץ.
מרווחים מוסיקליים
צירופי צלילים מסויימים הם נעימים לאוזן האנושית, ואילו אחרים צורמים. לפיתגורס, המתמטיקאי היווני, מיוחסת התגלית כי צירופי הצלילים הנעימים לאוזן מצייתים לחוקיות מתמטית. במונחים של דיוננו עד כה, תגליתו של פיתגורס אומרת כי זוג צלילים המושמעים בעת ובעונה אחת ישמע "נעים במיוחד" אם היחס המספרי בין תדירויותיהם הוא 2:1 או 3:2. בדוגמה 4 ניתן לשמוע - בהתחלה בנפרד, ואז ביחד - שני צלילים שתדירויותיהם הן 440 ו- 880 הרץ. המרווח המוסיקלי בין זוג צלילים כגון אלה, שיחס התדירויות ביניהם הוא 2:1, נקרא אוקטבה, והוא בעל חשיבות רבה במוסיקה, עליה נתעכב בהמשך. המרווח בין זוג צלילים שיחס תדירויותיהם הוא 3:2 נקרא קווינטה (דוגמה 5; התדירויות הן 440 ו- 660 הרץ).

פיתגורס
פיתגורס ותלמידיו פיתחו תורה שלמה הקושרת בין מספרים, צלילים מוסיקליים ותנועת גרמי השמיים. חלקים רבים ממשנתו נתפשים כיום כמיסטיקה אזוטרית, אך אלה העוסקים בחוקיות המספרית שמאחורי הצלילים מהווים עד היום, כ- 2,500 שנה לאחר שנוסחו, את הבסיס לתאוריה של המוסיקה.
מהי מנגינה?
סידרת צלילים המושמעים זה אחר זה נקראת מנגינה. הקשיבו למנגינה הקצרצרה שבדוגמה 6, בה משתתפים שלושה צלילים שתדירויותיהם הן 440, 660 ו- 733.3 הרץ. כעת הקשיבו לדוגמה 7, שתדירויות צליליה הן 550, 825 ו- 916.6 הרץ. האם זוהי אותה המנגינה? למרות ששתי המנגינות השתמשו בצלילים שונים לחלוטין, אנו מזהים בקלות ש"זו בעצם אותה המנגינה".
מה יצר את התחושה ש"זו בעצם אותה המנגינה"? מילת המפתח היא שוב יחסים. האוזן והמוח האנושיים, מסתבר, מזהים שתי סדרות של צלילים כ"אותה המנגינה" אם היחסים בין תדירויות צליליהן נשמרים. וזה, אכן, בדיוק מה שקרה: בשתי המנגינות, היחס בין תדירות הצליל הראשון לשני הוא 2:3, ובין הראשון לשלישי הוא 3:5.
גם הקול האנושי וגם כלי־נגינה הם מוגבלים בטווח התדירויות של הצלילים שהם מסוגלים להפיק. פעמים רבות, למשל, זמר מעדיף לשיר שיר מסוים "יותר גבוה" (או בלשון המוסיקאים, בסולם גבוה יותר) משום שהוא מתקשה לשיר היטב את הצלילים הנמוכים. המשמעות המתמטית של פעולה זו אמורה כעת להיות מובנת: הזמר פשוט ישיר צלילים שתדירויותיהם ימצאו ביחס קבוע עם תדירויותיהם של צלילי המנגינה המקורית. פעולה זו של שינוי סולם נקראת טרנספוזיציה.
האוקטבה
אם נאזין למנגינה המנוגנת בו זמנית בשני סולמות שונים, התוצאה תהיה על פי רוב "מוזרה", כפי שניתן להווכח בדוגמה 8. בדוגמא זו, המנגינה שתדירויות צליליה הן 440, 660 ו- 733.3 הרץ הושמעה במקביל לזו שתדירויותיה הן 550, 825 ו- 916.6 הרץ. אם, לעומת זאת, שתי המנגינות הן בדיוק במרחק של אוקטבה זו מזו (דהיינו, תדירויות צלילי האחת הן בדיוק כפליים מתדירות צלילי האחרת), התוצאה תהיה דווקא עשירה ונעימה לאוזן (דוגמה 9; בדוגמא זו מנגינה אחת השתמשה בתדירויות 440, 660 ו- 733.3 הרץ, והאחרת ב- 880, 1320 ו- 1466.6 הרץ).
האוזן האנושית מתייחסת לצלילים הנמצאים במרחק של אוקטבה זה מזה כ"אותו הדבר" במובן חזק ביותר, עד כדי כך שמוסיקאים העניקו לצלילים שכאלה את אותו השם. כזכור, הצליל שתדירותו 440 הרץ נקרא "לה", וזהו אכן גם שמו של הצליל שנמצא אוקטבה גבוה יותר (880 הרץ), שתי אוקטבות גבוה יותר (1760 הרץ), אוקטבה נמוך יותר (220 הרץ), וכו'. היות שצלילים המרוחקים זה מזה בדיוק כדי אוקטבה הם קשורים בקשר כה הדוק, מלחינים ומעבדים מוסיקליים נוהגים לעתים "להכפיל" את המנגינה המקורית, ולנגן במקביל אליה את אותה המנגינה, אוקטבה גבוה (או נמוך) יותר, לעתים על ידי מספר כלי־נגינה שונים. טכניקה זו יוצרת אפקט של "עושר", כפי שניתן לשמוע בדוגמה 10 ובדוגמה 11.
בעיית הכוון: באילו צלילים נבחר?
כלי־הנגינה השונים נבדלים זה מזה באופן בו הם מפיקים צלילים. מכינור, גם אם נותר בו רק מיתר אחד, ניתן להפיק אין־סוף צלילים: גובה הצליל נקבע לפי מיקום אצבע הכנר על צוואר הכינור (הקרוי "שחיף"), והיות שהשחיף הוא חלק, הכנר יכול להניח את אצבעו בכל מקום שיבחר, וכך להפיק צלילים שונים זה מזה כרצונו.
לפסנתר, לעומת זאת, יש מספר מוגבל של קלידים, ולכן הוא יכול להפיק רק מספר מוגבל של צלילים. אילו צלילים, אם כך, הם יהיו? הבה ננסה לענות על שאלה זו, ונצטמצם לאוקטבה שבין 440 ל- 880 הרץ. נתחיל בכך שנשים בתוך "סל הצלילים", אותם היינו רוצים שהפסנתר יוכל להפיק, את התדירות 440 הרץ. אם אנו מעוניינים להיות מסוגלים להשתמש ביחסים הפיתגוראיים המדוייקים, אזי בוודאי נצטרך להוסיף לסל את התדירות 660 הרץ, משום שראינו כבר שהיחס בין 660 ל- 440 הוא 3:2; במילים אחרות, 660 נמצא קווינטה מעל 440, אנחנו מעוניינים להיות מסוגלים לנגן בפסנתר קווינטות, ולכן 660 "בפנים". קווינטה נוספת מעל 660 נמצא 990; אמנם תדירות זו היא כבר מחוץ לתחום שלנו, אבל אוקטבה מתחתיה נמצא 495, שהוא בתוך התחום (ואנו מעוניינים להיות מסוגלים לנגן אוקטבות), ולכן 495 בפנים גם. עוד קווינטה מעל 495 נמצא 742.5, ולכן נוסיף גם אותו, וכך הלאה.
ניתן להראות שאם נמשיך בדרך זו, לעולם לא "נסגור מעגל" ונגיע שוב ל"לה" (דהיינו, לתדירות 440 או 880), ולכן נזדקק לאין־סוף צלילים בתחום המבוקש! זוהי אכן בעיה קשה, ודורות של מוסיקולוגים התווכחו בלהט כיצד לפתור אותה, והציעו שפע של שיטות לכוון המקלדת. מבלי להכנס לפרטים, נציין רק כי כלי־מקלדת עתיקים כוונו לרוב כך שהם אכן הפיקו מספר מסויים של מרווחים פיתגוראיים מדוייקים, אך כתוצאה מכך לא היה ניתן לנגן עליהם כראוי את אותה המנגינה בסולמות שונים (או במילים אחרות, לבצע טרנספוזיציות).

(צילום: באדיבות בוב הרן)
הפתרון: הכוון המושווה
הפתרון המודרני לבעיית הכוון מקריב את היכולת לנגן את המרווחים הפיתגוראיים בדיוק מוחלט תמורת היכולת לבצע טרנספוזיציות באופן מושלם. הרעיון שבבסיסו הוא לחלק את האוקטבה למספר כלשהו של מרווחים מוסיקליים שווים בגודלם.
נניח שהיינו רוצים לחלק את האוקטבה שבין 440 ל- 880 הרץ לשני מרווחים מוסיקליים שווים בגודלם. כזכור, גודלו של מרווח מוסיקלי נקבע על פי היחס שבין תדירויות הצלילים המרכיבים אותו, כך שאנו מחפשים מספר בין 440 ל- 880 שהיחס בינו לבין 440 שווה ליחס בין 880 לבינו. חישוב קצר מעלה שהיחס המבוקש הוא השורש של 2, כך שתדירות הצליל שב"אמצע" האוקטבה היא 440 כפול שורש 2, או 622.25 הרץ.
באופן דומה, אילו היינו רוצים לחלק את אותה אוקטבה לשלושה מרווחים מוסיקליים שווים בגודלם, היינו מקבלים כי יחס התדירויות בין שני צלילים סמוכים בחלוקה הוא השורש השלישי של 2. לכן, ב"שליש הדרך" שבין 440 ל- 880 נמצאת התדירות 440 כפול השורש השלישי של 2, שהיא 554.37 הרץ, וב"שני שליש הדרך" נמצאת תדירות אחרונה זו כפול (שוב) השורש השלישי של 2, דהיינו 698.46 הרץ.
ניתן, כמובן, לחלק את האוקטבה בצורה שכזו גם לארבעה, חמישה, או כל מספר אחר של מרווחים שווים. חשוב לציין כי ברגע שחילקנו אוקטבה אחת בצורה מסויימת, אנחנו מקבלים מיד גם את תדירויות הצלילים שבאוקטבות השכנות - כשחילקנו את האוקטבה לשלושה חלקים, למשל, התדירויות שתתקבלנה באוקטבה שבין 880 ל- 1760 הרץ הן פשוט כפליים מהתדירויות שמצאנו לעיל, דהיינו 880, 1108.73, 1369.91 ו- 1760.
היתרון החשוב שבחלוקת אוקטבה למספר מסוים של מרווחים שווים הוא שניתן אז לבצע טרנספוזיציות באופן מושלם: היות שהקפדנו שהיחס בין צלילים סמוכים שנוצרו בחלוקה יהיה קבוע, נוכל לקחת כל מנגינה הניתנת לנגינה על הפסנתר ש"יצרנו", להכפיל את תדירות צליליה ביחס זה, ולקבל שוב מנגינה אותה נוכל לנגן על אותו הפסנתר; כך שמרנו על היחסים בין תדירויות הצלילים, וקיבלנו את "אותה המנגינה", רק בסולם אחר.
החסרון שבשיטה זו הוא שהמרווח הפיתגוראי המדוייק היחיד אותו נהיה מסוגלים לנגן הוא האוקטבה. ניתן לבדוק ולראות כי לא משנה לכמה חלקים שווים נחלק את התחום שבין 440 ל- 880, החלוקה לעולם לא תכלול את התדירות 660, הנמצאת, כזכור, בדיוק קווינטה מעל 440. במבט ראשון, בעייה זו נראית חמורה - המרווחים הפיתגוראיים הם בעלי חשיבות מוסיקלית עצומה, ולא היינו רוצים לאבד את היכולת להשתמש בהם. הישועה במקרה זה צומחת דווקא ממגבלותיה של האוזן האנושית: אמנם לעולם לא נצליח להגיע בדיוק לתדירות 660, אבל חלוקה זהירה של האוקטבה למספר "הנכון" של מרווחים שווים תגרום לאחת התדירויות שתתקבלנה להיות קרובה מאוד ל- 660 - קרובה עד כדי כך שיהיה לנו קשה מאוד להבחין בין שני הצלילים.
לכמה מרווחים, אם כך, כדאי לחלק את האוקטבה? מספר הקסם, מסתבר, הוא 12. אם נחלק את האוקטבה לשנים־עשר מרווחים שווים בגודלם (ואז יחס התדירויות בין שני צלילים סמוכים יהיה השורש ה- 12 של 2), התדירויות שתתקבלנה הן: 440, 466.16, 493.88, 523.25, 554.37, 587.33, 622.25, 659.26, 698.46, 739.99, 783.99, 830.61, ו-880. כצפוי, בין תדירויות אלה לא נוכל למצוא את 660, אבל כן את 659.26, הנמוכה ממנה אך במעט. בדוגמה 12 ניתן לשמוע את שני הצלילים האלה, זה אחר זה; התוכלו לזהות האם הצליל הנמוך מבין השניים הוא הראשון או השני? (תשובה מוצפנת: מיקום הצליל הנמוך הוא כמיקום האות ב' במילה הראשונה בגוף מאמר זה.) באופן דומה, ניתן למצוא ברשימת תדירויות זו גם "תחליפים קרובים" (אם כי לא כה קרובים) לשאר התדירויות שב"סל הצלילים" שבנינו לעיל.
שיטת כוון זו, בה האוקטבה מחולקת לשנים עשר מרווחים מוסיקליים שווים בגודלם, נקראת "כוון מושווה" (equal temperament), ובתחילת המאה העשרים היא דחקה כמעט לחלוטין את רגליהן של אין ספור שיטות כוון אחרות שהוצעו במהלך הדורות. למרות הדמיון בשם העברי, ובניגוד לאמונה הנפוצה למדי, שיטה זו אינה זהה לזו שלכבודה חיבר באך את "הפסנתר המושווה". באך, כפי הנראה בהשראת המוסיקולוג אנדריאס ורקמייסטר (Werckmeister), אמנם השתמש בשיטת כוון שחילקה את האוקטבה לשנים עשר מרווחים, אך מרווחים אלה היו שונים מעט בגודלם; שיטה זו נחשבה בתקופתו לחדשנית משום שהיתה בין הראשונות לאפשר בצוע טרנספוזיציה סבירה (אם כי לא מושלמת) של כל מנגינה לאחד־עשר סולמות אחרים.
לשם ההשוואה, הקשיבו לארבע התיבות הראשונות של הפרלוד הראשון של באך מתוך "הפסנתר המושווה" בכוון פיתגוראי (דוגמה 13), בכיוון של ורקמייסטר (דוגמה 14) ובכוון מושווה (דוגמה 15). ההבדלים במקרה זה אינם בולטים, משום שהיצירה נכתבה בסולם בו הכוון הפיתגוראי מצלצל במיטבו. אם ננגן תיבות אלה בסולם אחר, הכוון הפיתגוראי (דוגמה 16) אכן יישמע צורם הן יחסית לכוון של ורקמייסטר (דוגמה 17), והן יחסית לכיוון המושווה (דוגמה 18).
היות שחלוקת האוקטבה של באך לא היתה שוויונית לחלוטין, יש הטוענים שכל סולם שנוצר על ידה ניחן ב"צבע" משלו שאבד בכלי־הנגינה של ימינו; לכן, לדעתם, עדיף לנגן יצירות מוסיקליות בכלים המכוונים בשיטה שרווחה בעת חיבורן. גם אחרים אינם מרוצים מהכוון המושווה שתואר לעיל: במוסיקה הערבית מרובת הניואנסים אין די בחלוקת האוקטבה לשנים עשר מרווחים, והיא לפיכך מחולקת לעשרים וארבעה מרווחים שווים; ישנם הסבורים כי גם המוסיקה המערבית צריכה להתפתח לכוונים "מיקרוטונליים", ומחלקים את האוקטבה לשלושים־ואחד מרווחים (כך זה נשמע), ואילו אחרים גורסים כי יש לחזור לכוון המתבסס על היחסים הפיתגוראיים הטהורים.
ומה צופן העתיד? הנבואה, כידוע, היא מלאכה קשה, אך סביר להניח כי המצב הנוכחי ישאר על כנו - הכוון המושווה ימשיך לשלוט, אך הויכוחים יימשכו, ושיטות מתחרות תמשכנה למצוא אוהדים מחוץ לזרם המוסיקלי המרכזי.
תודה עמוקה מגיעה לאלון עמית, על מיומנותו המוסיקלית והטכנית בהכנת קבצי הקול והגרפים למאמר.
|
קישורים
הפסנתר המושווה - יצירתו של באך
ישנם הסבורים כי מיקרוטונליות עדיפה
כך זה נשמע - מוזיקה מערבית מיקרוטונלית
אחרים גורסים כי פיתגורס עדיף
|
|
 |






 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות




