תורת הקוונטים ידועה כמוצלחת ביותר מבחינה ניסויית. טרם נעשה ניסוי שמפריך אותה, להפך: ככל שגדלה יכולתנו לבצע ניסויים, כך גדל הדיוק שבו תחזיותיה מתבררות כנכונות. ועם זאת, כידוע היא מוזרה מאוד מבחינת האינטואיציה האנושית. אולי פחות ידוע שמעבר לאינטואיציה שלנו, היא מעוררת בעיות גם בתחום התיאורטי. סדרת מאמרים זו תעסוק בבעיה שהיא אולי הקשה שבהן: בעיית המדידה, המעסיקה פיזיקאים ופילוסופים כאחד.
כדי שנוכל להציג את בעיית המדידה, עלינו להבין מה אומרת תורת הקוונטים. וכדי להבין מה אומרת תורת הקוונטים, וגם למה - בשביל מה צריך תיאוריה מוזרה כזו - עלינו לתאר כמה ניסוים, ואת תוצאותיהם המפתיעות.
נוח מאוד לעבוד עם ניסוי שטרן־גרלאך (Stern-Gerlach) ופיתוחיו השונים. זהו ניסוי פשוט ביותר לתיאור סכמטי, ומוביל אותנו היישר אל המסתורין הקוונטיים.
בניסוי של שטרן וגרלאך יורים אלקטרונים, כך שבקטע של מסלולם פועל שדה מגנטי בכיוון מסוים. מתברר כי האלקטרונים מתפצלים לשני מסלולים: חלקם ממשיכים למעלה, וחלקם למטה (היחס יכול להשתנות בהתאם למקור של האלקטרונים). רואים זאת אם שמים לוח צילום מאחורי השדה המגנטי: הלוח יראה פגיעות של אלקטרונים סביב שתי נקודות בלבד. לחילופין, אנו יכולים לשים גלאי אלקטרונים בנקודות שונות במרחב; הגלאים יעשו "קליק" רק אם הם נמצאים על אחד משני המסלולים.
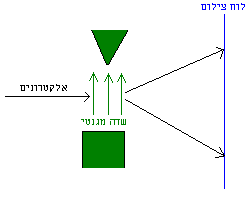
ניסוי 1
נניח כעת שבמסלולם של האלקטרונים שיצאו למעלה אנו שמים שדה מגנטי נוסף, באותו כיוון. נקבל שכל האלקטרונים סוטים שוב למעלה:
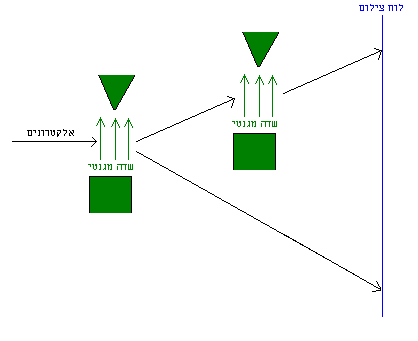
ניסוי 2
(הציור משקר קצת, לצורך הפשטות בהמשך: נראה כאילו האלקטרונים יוצאים מהשדה השני באותו כיוון בו הם נכנסו אליו. למעשה, הם יוצאים בזוית חדה יותר למעלה, כלומר מקבלים סטייה ביחס לכיוון תנועתם הקודם). אנו יכולים להמשיך ולשים עוד שדות מגנטיים באותו כיוון, ונקבל תמיד שהאלקטרונים סוטים למעלה. באותו אופן, אם נעשה זאת עבור האלקטרונים שיצאו למטה מהשדה הראשון, נקבל שהם ממשיכים לסטות למטה. מכאן, נראה שמדובר בתכונה של האלקטרונים, בחלוקה שלהם לשני סוגים: אלו שפונים למעלה ואלו שפונים למטה בהשפעת שדה מגנטי בכיוון מסוים; השדה הראשון סינן את אלו בעלי התכונה לסטות למעלה.
לתכונה הזו קראו הפיזיקאים "ספין". הסיבה לשם היא שאופי תנועה כזה בהשפעת שדה מגנטי אופייני לגופים טעונים שמסתובבים סביב צירם. אך יש לציין שמכל הידוע לנו על האלקטרון, אין משמעות לדבר עליו כעל גוף המסתובב סביב צירו - קשה בכלל לדבר עליו כעל גוף מוגדר בעל צורה במרחב. עדיף להתייחס לספין כאל תכונה מופשטת, שאיננו יודעים עליה יותר מאשר ההתנהגות של האלקטרונים בשדה מגנטי: יש אלקטרונים עם "ספין מעלה", ויש עם "ספין מטה". אפשר לדבר על "מדידה של הספין", ופירוש הדבר פשוט העברה של האלקטרון בשדה מגנטי בכיוון מתאים, ובדיקה לאן הוא סטה.
נניח כעת שבמסלולם של האלקטרונים שיצאו למעלה מהשדה הראשון אנו שמים שוב שדה מגנטי, אבל שכיוונו שונה בתשעים מעלות לזה של השדה הראשון. נקרא לכיוון של השדה הראשון x ושל השני y. שוב נקבל פיצול לשני מסלולים. אבל כאן יש תוצאה נוספת, מפתיעה אולי: האלקטרונים מתפצלים ביחס חצי־חצי בדיוק (עד כמה שאנו מסוגלים למדוד בדיוק):
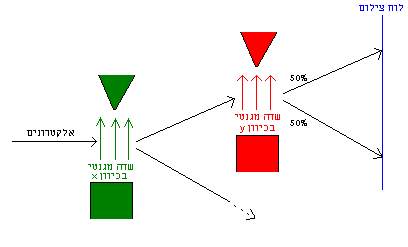
ניסוי 3
התוצאה חצי־חצי אינה תלויה בחלוקה הראשונית של האלקטרונים (שכזכור, תלויה במקור שלהם, ובעצם אינה מעניינת לצרכינו). כפי שניתן לנחש, תופעה זהה תקרה אם נשים את השדה-y במסלול של אלו שיצאו למטה מהשדה-x. חשוב לציין גם שמדובר בחלוקה סטטיסטית: אנו יכולים לשגר את האלקטרונים אחד־אחד, ועבור כל אחד שיצא למעלה מהשדה-x לרשום לחוד האם יצא מהשדה-y למעלה או למטה; אם נעשה זאת פעמים רבות, נגלה שהיחס מתקרב לחצי־חצי, אולם איננו יודעים לחזות מראש, לפי שום נתונים, איזה אלקטרון ייצא למעלה ואיזה למטה.
אם נשים במסלול של האלקטרונים שיצאו למעלה מהשדה-y שדה נוסף (שלישי) בכיוון y, כל האלקטרונים יסטו למעלה:
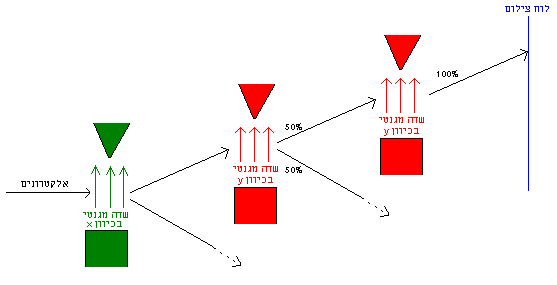
ניסוי 4
וכך גם אם נשים שדות רבים באותו כיוון, אחד אחרי השני. כלומר, נראה שיש לנו כאן תכונה נוספת של האלקטרון. לאלקטרון יש ספין-x 'מעלה' או 'מטה', וספין-y 'מעלה' או 'מטה'. אך יש תלות בין התכונות: אלקטרונים שהם ספין-x 'מעלה' מתחלקים חצי־חצי בין ספין-y 'מעלה' וספין-y 'מטה', וכך גם אלקטרונים שהם ספין-x 'מטה'.
כפי שאפשר לנחש, היינו מקבלים תוצאות מקבילות אם היינו הופכים את סדר השדות: אלקטרונים שהם ספין-y 'מעלה' מתחלקים חצי־חצי בין ספין-x 'מעלה' וספין-x 'מטה', וכו'.
לצורך דברים שיקרו בחלקים הבאים של המאמר, נציין מה קורה כאשר השדה השני אינו בתשעים מעלות לשדה הראשון (x ו-y) וגם לא מקביל לו (x ו-x), אלא בזוית אחרת כלשהי. כאן האלקטרונים יתפצלו לשניים, אך ביחס שונה מחצי־חצי. היחס יהיה תלוי בזוית: אם בדקנו אלקטרונים שיצאו למעלה מהשדה הראשון, אז ככל שהכיוון של השדה השני יהיה שונה יותר מזה של השדה הראשון, היחס ייטה יותר לטובת 'מטה': למשל, בזוית 60 מעלות 3/4 מהאלקטרונים יצאו מעלה. בזוית 90 מעלות (שדה-y), כאמור היחס הוא חצי; בזוית 120 מעלות, רבע יצאו מעלה; ולבסוף, בכיוון 180 מעלות (שדה הפוך בכיוונו לראשון), יצאו כולם מטה.
מה יקרה אם ניקח אלקטרונים שיצאו למעלה מ-x ולמעלה מ-y, ונשים להם שדה שלישי, אבל הפעם שוב בכיוון x? היינו אולי מצפים, מכיוון שמדובר לכאורה באלקטרונים עם ספין-x 'מעלה', שהם יצאו כולם למעלה. הפלא ופלא: הם מתפצלים שוב חצי־חצי:
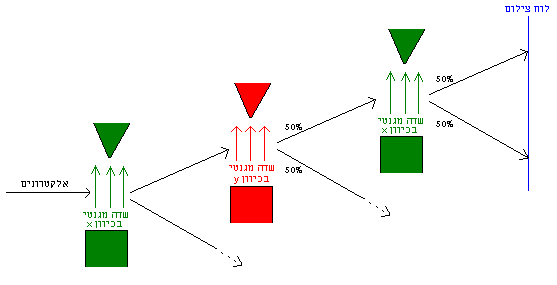
ניסוי 5
כלומר, המדידה של ספין-y "הרסה", כך נראה, את הספין-x של האלקטרון. "תכונת" הספין נשמרת בדיוק עד מדידת הספין הבאה. מדידה של ספין (בכיוון כלשהו) קובעת בדיוק (אם גם באופן סטטיסטי בלבד) את תוצאות המדידה הבאה של ספין כלשהו, אך "מנטרלת" כל מדידה קודמת.
כעת, נשנה קצת את התרגיל: ניקח אלקטרונים שאנו יודעים שהם בעלי ספין-x 'מעלה', ונעביר אותם בשדה מגנטי y כך שהם יתפצלו חצי־חצי. אז נאחד שוב את שתי האלומות, ע"י כך שנסיט אותן (בעזרת שדה מגנטי אחר, שישמש כ"מראה"). לבסוף, בנקודת המפגש שלהם, נמדוד שוב ספין-x. הפעם נקבל שכולם ספין-x 'מעלה':
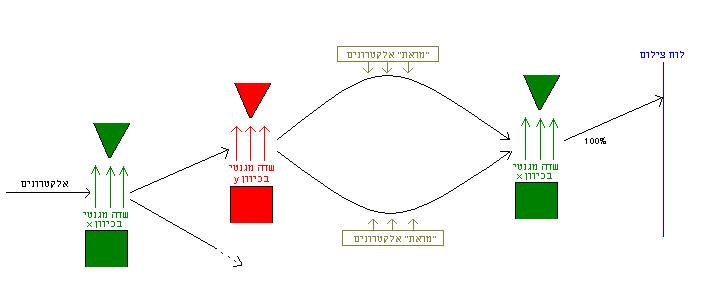
ניסוי 6
מה קרה כאן? הפעם נראה שהאלקטרונים "זכרו" את הספין-x שלהם, למרות שמדדנו להם ספין-y! אבל אי־אפשר לומר בדיוק ש"מדדנו" ספין-y, שהרי איננו יודעים, עבור כל אלקטרון, באיזה כיוון הוא יצא מהשדה-y. מה שאנו רואים כאן הוא שלא עצם המעבר בשדה מגנטי y מקלקל את הספין-x; צריך, כך נדמה, לדעת מהו הספין-y.
אנו יכולים להתחכם, וכן לדעת מהו הספין-y, אם פשוט נחסום את אחד משני המסלולים - נניח, התחתון. אז נדע שהאלקטרונים שהגיעו לשדה-x הם בעלי ספין-y 'מעלה'. אלא שאז, הפלא ופלא -
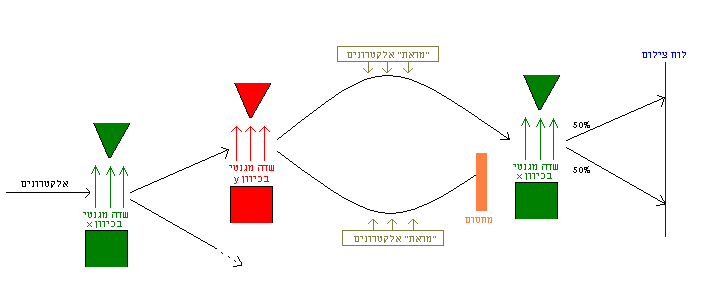
ניסוי 7
האלקטרונים מתפצלים חצי־חצי. הפעם אפשר שוב לדבר על "מדידה" של ספין-y, כי אנו כבר יודעים באיזה מסלול האלקטרונים עברו. לכן אפשר עדיין להחזיק בטענה שלנו מקודם, לפיה מדידה של ספין-y "מקלקלת" מדידה קודמת של ספין-x. וכמובן, תוצאה זהה תתקבל אם נשים את המחסום במסלול העליון.
אולי אפשר להסביר את ההבדל בין ניסוי 6 ל-7 בכך שבניסוי 6 האלקטרונים משני המסלולים העבירו איכשהו אינפורמציה זה לזה כאשר הם נפגשו? קשה, אם נזכור כי לא מדובר בהכרח באלומה של המוני אלקטרונים: אנו יכולים לעשות את הניסויים עם אלקטרונים בודדים, אחד בכל פעם. באופן סטטיסטי, נקבל את אותן תוצאות: בניסוי 7, בחצי מהמקרים (ואיננו יודעים לחזות אילו) נמדוד לאלקטרון ספין-x 'מעלה', ובחצי ספין-x 'מטה'; ובניסוי 6, ללא מחסום, נקבל תמיד ספין-x 'מעלה'.
יש לציין כי את כל הניסויים האלו יש לבצע בסביבה "סטרילית", לא רק בואקום אלא גם בבידוד מאור. התנגשויות של פוטונים (חלקיקי אור) באלקטרונים יהרסו את המסלולים של אלו. אבל דווקא על־ידי שיגור מבוקר של פוטונים בודדים, ומעקב אחרי מסלולם, אפשר לפעמים "לעקוב" אחרי האלקטרון הבודד מבלי להפריע לו יותר מדי: יש סיכוי לדעת דרך איזה מסלול יצא האלקטרון מהשדה-y, וכך שבכל זאת האלקטרון יגיע לשדה-x (ונמדוד לו ספין-x). אם נעשה זאת, נקבל תוצאה דומה למקרה המחסום: אם אנו יודעים שהאלקטרון עבר מלמעלה (בגלל שהוא הגיב שם עם פוטון), אז בהכרח נמדוד לו ספין-x 'מעלה'. אם אנו יודעים שהאלקטרון עבר מלמטה (מסיבה דומה), גם אז נמדוד לו ספין-x 'מעלה'. אבל אותם אלקטרונים שלא הגיבו עם פוטון, ואיננו יודעים דרך איזה מסלול הם עברו, יתחלקו חצי־חצי בין שני ערכי הספין-x.
אם כן, נראה שאנו מגיעים למסקנה הבאה: לשאלה אם אנו יודעים משהו על האלקטרון יש השלכות פיזיקליות על ההתנהגות שלו: כאשר אנו יודעים שהוא עבר למעלה, או עבר למטה, הוא מתנהג באופן מסוים; כאשר איננו יודעים, הוא מתנהג באופן אחר. אבל כאן כבר צריך להיזהר עם המונחים, ולא לקפוץ למסקנות מטאפיזיות. לעתים אומרים שהתודעה של הצופה משפיעה על הניסוי; זה קצת פזיז. אפשר לעשות את הניסויים ללא צופה אנושי בכלל, כאשר התוצאות פשוט ירשמו, למשל, בפלט מחשב. אם נסתכל על פלט המחשב, שעות רבות לאחר שהניסוי הסתיים, נראה תוצאות זהות לאלו שאנו רואים כאשר אנו עוקבים אחרי הניסוי בזמן אמת.
מסקנה יותר שמרנית מהניסויים תהיה, ש"הידיעה" המשפיעה על הניסוי אינה בהכרח צופה בעל תודעה שיודע, אלא כל שינוי של מצב העניינים בעולם, שינוי המאפשר עקרונית שצופה ידע. מחוג של מכשיר מדידה זז, דיו נרשם על ניר מדפסת, נקודת אור נרשמת על לוח־צילום - אלו שינויים במצב העניינים בעולם שאפשר לקרוא להם "ידיעה", לצורך הדיון שלנו בינתיים. בהמשך סדרת המאמרים נראה שישנן תיאוריות שכן מייחסות חשיבות לתודעה; אבל גם אז יש לעשות זאת יותר בזהירות, להבין מה בדיוק אומרים, ומה הסיבה לכך.
מכל מקום, האינטואיציה האנושית נכנסה כבר לקשיים ניכרים. בניסוי 6 איננו יודעים דרך איזה מסלול עברו האלקטרונים לאחר השדה-y. אבל הרי טבעי לחשוב שהם עברו או מלמעלה, או מלמטה, ואין אפשרויות אחרות - הרי אם אנו בודקים זאת, בכל דרך שיש לנו, אנו תמיד רואים אחת משתי האפשרויות! ועם זאת, בניסויים שבהם האלקטרון עובר מלמעלה, יש לו התנהגות מסוימת (ספין-x 'מעלה'), וגם בניסויים שבהם הוא עובר מלמטה יש לו אותה התנהגות (ניסוי 7); ואילו בניסוי שלנו - ההתנהגות שונה (ספין-x מתחלק חצי־חצי).
אם כן, מה עושה תורת הקוונטים עם המצב הזה? נותנת לו שם: "סופרפוזיציה". בניסוי 6, אנו אומרים כי האלקטרון לאחר השדה-y נמצא "בסופרפוזיציה של שני המסלולים" - כלומר, בכל רגע הוא נמצא "בסופרפוזיציה של שני מקומות", אחד במסלול העליון ואחד במסלול התחתון. אפשר לומר, לחילופין, שהוא בסופרפוזיציה של ספין-y 'מעלה' וספין-y 'מטה'. אין פירוש הדבר שהאלקטרון הוא "או עם ספין מעלה או עם ספין מטה"; איננו רוצים לומר דבר כזה, שהרי ראינו שכאשר הוא בכל אחד משני המצבים, הוא מתנהג בצורה מסוימת, וזו אינה ההתנהגות של המצב שאנו קוראים לו סופרפוזיציה. אפשר לומר שהסופרפוזיציה פירושה שהאלקטרון הוא "גם עם ספין מעלה וגם עם ספין מטה", אבל אין בכך טעם רב, כי לא ברור מה זה אומר. באותו אופן, "להיות בסופרפוזיציה של מקום א' ומקום ב"' אין פירושו "להיות או בנקודה א' או בנקודה ב"': זהו מצב שונה. נראה שאין לנו דרך לתאר סופרפוזיציה במונחים שמוכרים לנו מחיי היומיום, שבהם לגופים יש מקום מוגדר במרחב, או מסלול מוגדר במרחב ובזמן.
המודל המתמטי של תורת הקוונטים
תורת הקוונטים עושה, כמובן, יותר מלהגיד "סופרפוזיציה": היא נותנת מודל מתמטי שלם, שמתאר את הניסויים הללו, והמון ניסויים אחרים (שגם בהם קורות תופעות מוזרות, של התנהגות פיזיקלית של חלקיקים המושפעת, כך נראה, ממדידות). משותף לכל הניסויים שהם עוסקים במערכות קטנות: אלקטרונים בודדים, פוטונים, וכדומה. אבל לעתים להתנהגות "קוונטית" של חלקיקים בודדים יש השפעה על מערכות גדולות - כידוע, בלב שבב המחשב, למשל, נמצאים רכיבים המבוססים על אפקטים קוונטיים.
נציג כמה מושגים חשובים מהמודל המתמטי, שישמשו אותנו בהמשך. המודל מטפל לאו דווקא בחלקיקים כאלה או אחרים, אלא ב"מערכת". המערכת יכולה להיות חלקיק, או זוג חלקיקים, או כל אוסף אחר (וגם גופים גדולים). בניסויים שתיארנו המערכת היא אלקטרון. המושג המתמטי המתאר מערכת נקרא "פונקציית גל" (המילה "גל" נכנסה לכאן מסיבות היסטוריות ומתמטיות בעיקר, ולא כדאי להתעכב עליה). פונקציית הגל מציגה, לרוב, את המערכת כסופרפוזיציה של גדלים. בניסוי 6, פונקציית הגל של האלקטרון לאחר השדה-y היא סופרפוזיציה של ספין-y 'מטה' וספין-y 'מעלה'.
פונקציית הגל של מערכת משתנה בזמן, על־פי הכוחות והאילוצים הפיזיקליים (למשל, שדות מגנטיים או קירות). ההשתנות בזמן מתוארת על־ידי "משוואת שרדינגר". כלומר, אם נכניס למשוואה את הכוחות והאילוצים, ואת פונקציית הגל בזמן מסוים, תאמר לנו המשוואה מה תהיה פונקציית הגל בכל זמן מאוחר יותר.

ארווין שרדינגר (פרט מתוך שטר של 1,000 שילינג אוסטרי)
המודל עבור ספינים הוא, שספין-x 'מעלה' הוא סופרפוזיציה של ספין-y 'מעלה' וספין-y 'מטה'; זהו מצב אחד, בעל פונקציית גל אחת, ואת שני סוגי הספינים אפשר לראות כשני היבטים שלו: המצב הוא חד־ערכי מבחינת הספין-x, ודו־ערכי מבחינת הספין-y. ספין-x 'מטה' הוא מצב שונה, אך גם הוא סופרפוזיציה של שני ערכי ספין-y. באותו אופן, ספין-y 'מעלה' (מצב שונה, שלישי) הוא סופרפוזיציה של ספין-x 'מעלה' וספין-x 'מטה'. אם אלקטרון במצב ספין-x 'מעלה' נכנס לשדה-x, אז הוא מוסט למעלה; ואם הוא במצב ספין-x 'מטה' אז הוא מוסט למטה.
בניסוי 3 נכנס לשדה-y אלקטרון בספין-x 'מעלה'. מכיוון שהוא בסופרפוזיציה של שני ערכי ספין-y, הוא יוצא בסופרפוזיציה של שני המסלולים, כלומר נמצא, בכל רגע אחר־כך, בסופרפוזיציה של שני מקומות. כך גם בניסוי 6; אבל שם אנחנו מביאים את האלקטרון שוב לשדה-x. פונקציית הגל שלו לא השתנתה, והיא עדיין ספין-x 'מעלה' - חד ערכית בספין-x, ולא בסופרפוזיציה. לכן, המסלול שלו נהיה שוב פשוט, ולא בסופרפוזיציה.
אבל הסופרפוזיציה אינה כל התמונה. אפילו בניסוי 1 יש לומר משהו נוסף. האלקטרון יוצא שם מהשדה בסופרפוזיציה של שני מסלולים - אבל בסופו של דבר, על לוח הצילום, אנו רואים פגיעה באחת משתי נקודות. מרכיב אחר בתורת הקוונטים הוא המדידה. כאשר אנחנו מבצעים מדידה של גודל שהוא בסופרפוזיציה בין כמה ערכים, אומרת תורת הקוונטים, המערכת "קורסת" לאחד הערכים - כלומר, "בוחרת" באחד מהם.
אי אפשר לדעת במקרה נתון לאיזה מהערכים היא תקרוס, אך ההסתברות לכל ערך ניתנת לחישוב מתוך פונקציית הגל: בסופרפוזיציה יתכן משקל שונה לערכים שונים. במקרה של ספין-x 'מעלה', הסופרפוזיציה של שני ערכי ספין-y היא במשקל שווה, ולכן ההסתברות לקריסה לכל אחד מהם תהיה חצי. זה מה שקורה בניסוי 3. הזכרנו שם שאם שני השדות המגנטיים אינם מאונכים זה לזה, ההסתברות לשני הערכים אינה מאוזנת; הביטוי המתמטי לכך הוא משקלים שונים בסופרפוזיציה. למעשה, ההסתברות לכל ערך היא פשוט הגודל המספרי של פונקצית הגל באותו ערך, מועלה בריבוע (הכלל הפשוט הזה נקרא "כלל בורן" (Born)).
רק עוד דבר אחד נותר להוסיף: להסביר את ניסוי 5 (או ניסוי 7; מבחינת תורת הקוונטים, הם שקולים). בניסוי זה מדדנו את הספין-y, והתוצאה השפיעה על המדידה הבאה של ספין-x. מה שאומרת על כך תורת הקוונטים הוא שהמדידה, והקריסה הכרוכה בה, משנות את פונקציית הגל של המערכת: פונקציית הגל החדשה לאחר המדידה היא פשוט פונקציית הגל שמתאימה לערך שנמדד. לשדה-y נכנסו אלקטרונים עם ספין-x 'מעלה', כלומר בסופרפוזיציה של ספין-y. שם ביצענו מדידה: מעצם זה שאנו מסתכלים אחר־כך רק על האלקטרונים שסטו למעלה, משמע שמדדנו להם את הספין-y. אנו מסתכלים על אלו שיש להם ספין-y 'מעלה'; משמע, פונקציית הגל שלהם קרסה למצב של ספין-y 'מעלה'. מצב זה, כזכור, הוא סופרפוזיציה של שני ערכי ספין-x; לכן במדידת ספין-x אנו מקבלים שתי תוצאות.
אחת התכונות של המודל המתמטי היא שייתכנו שתי תכונות שניתן למדוד כל אחת מהן לחוד, אולם לא ניתן למדוד את שתיהן ביחד, או לא ניתן לדעת את שתיהן ביחד. זהו "עקרון אי־הוודאות" המפורסם. זוג אחד כזה של תכונות הוא ספין-x וספין-y; ואכן, זה מתאים להתנהגות שראינו בניסוי 5 ואילך. זוג אחר של תכונות ביחסי אי־ודאות הוא המקום של חלקיק והמהירות שלו (או התנע, אם לדייק).
סיכום זמני, ומה צפוי לנו בהמשך
אפילו כשאומרים "תורת הקוונטים", יש להבהיר למה הכוונה. במובן כללי, מדובר בכל העיסוק הפיזיקלי בדברים שנידונו פה; במובן מצומצם, מדובר במודל המתמטי הספציפי שהוצג כאן ברפרוף. בהמשך סדרת המאמרים נראה פרשנויות ותיאוריות שמטפלות באותם ניסויים ובאותם מושגים, אבל אומרות דברים שונים ומשונים. תיאוריות אלו חורגות מתורת הקוונטים במובן המצומצם שלה, אך נשארות במסגרת העיסוק בה - למעשה כולן מגיבות עליה. אי־אפשר לחמוק מתורת הקוונטים: יש בה מושג בעייתי, לפחות לכאורה, של הסופרפוזיציה המסתורית, ומושג זה הוא לחלוטין פרי התיאוריה; אבל הוא בא לעולם כדי להסביר תוצאות שאנו רואים במעבדה. התיאוריה עושה זאת בהצלחה מרובה; כאשר מדובר על מדידות של גדלים מספריים, הניבויים שלה מדויקים להפליא. כנראה שיש בתורת הקוונטים לפחות משהו, גם אם לבסוף נשתכנע שהיא לא אומרת מספיק על העולם (או שהיא אומרת יותר מדי).
בחלק הבא (שיתפרסם בעוד כשבוע) נדון בניסויי EPR ובאי־שוויון בל, המציגים אילוצים מעניינים על תורת הקוונטים ועל פרשנויות לה. בחלק השלישי נציג, סוף סוף, את בעיית המדידה, המוקד של סדרת המאמרים, ושני פתרונות לה: הפתרון התודעתי של ויגנר, ותורת הקריסה של GRW. בחלק האחרון נציג את הפתרון של בוהם (Bohm), ואת משפחת הפתרונות שסביב תיאוריות העולמות המרובים.
תודה לד"ר מאיר חמו מאוניברסיטת חיפה על תרומתו לסדרת המאמרים.
|
קישורים
|






 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות








