 |
|
נתונים סטטיסטיים מקיפים אותנו מכל עבר, אבל לעתים קרובות מדי הם חלקיים, מטעים, או פשוט שגויים. על כמה כשלים סטטיסטיים נפוצים, וכיצד להתמודד איתם.
|
|
| מדע • יובל נוב • יום ד', 21/7/2004, 19:55 |
|
 |
|
| (צילום: iStockPhoto) |
|
"ישנם שלושה סוגים של שקרים: שקרים, שקרים נאלחים, וסטטיסטיקה" מספר פתגם ישן. אבל למרות המוניטין המפוקפקים של מדע הסטטיסטיקה, אנחנו חיים בעידן המקדש את הנתונים המספריים יותר מאי־פעם: פוליטיקאים, מדענים, עיתונאים ואנשי שיווק – כולם מנופפים בפנינו במספרים כדי לעצב את דעותינו, למשוך את תשומת־לבנו, או לגרום לנו לפתוח את ארנקינו.
קל מאד להשתמש בסטטיסטיקה באופן שגוי. טעויות סטטיסטיות נעשות לעתים בתום לב, אך לעתים גם בדעה צלולה, מתוך מטרה להוליך שולל. במאמר זה נסקור כמה מהכשלים הסטטיסטיים הנפוצים, ובסופו נציע גם מספר כללים ל"צרכנות סטטיסטית" נבונה.
מדגמים טובים ורעים
השלב המעשי הראשון בכל מחקר סטטיסטי הוא איסוף נתונים. נניח, לדוגמא, שאנו מעוניינים למצוא את משקלם הממוצע של אזרחיה הבוגרים של מדינת ישראל. הדרך המדויקת ביותר לעשות זאת – לעבור ביניהם אחד־אחד, לשקול אותם ולחשב את הממוצע – היא כמובן בלתי אפשרית טכנית. אין מנוס במקרה זה מלהשתמש במדגם: למדוד את משקלם של חברי קבוצה נבחרת, קטנה בהרבה, מקרב אזרחי המדינה, ולחשב את ממוצע המספרים שהתקבלו.
כדי שתוצאות המדגם תשקפנה כראוי את "הממוצע האמיתי" (זה של כל אזרחי המדינה), על המדגם לקיים שני תנאים חשובים. ראשית, עליו להיות גדול דיו – במדגם זעיר, די בנבדק אחד החורג משמעותית מהממוצע כדי לשבש לחלוטין את התוצאה. ניתן להראות מתמטית כי ככל שהמדגם גדול יותר, כך נוטות החריגות לקזז זו את זו, וההסתברות לכך שממוצע המדגם יהיה שונה במידה ניכרת מהממוצע האמיתי הולכת ומתקרבת לאפס.
שנית, על המדגם להיות מייצג. יהיה זה רעיון רע מאד, למשל, להשתמש לצורך המחקר בנתוני המשקל של המתגייסים לצה"ל, משום שהמתגייסים הם צעירים שלרוב טרם גידלו כרס, והם לכן רחוקים מלייצג כהלכה את כלל אזרחי המדינה. הפער שיתקבל במקרה כגון זה בין ממוצע המדגם לבין הממוצע האמיתי נקרא הטיה. ההטיה שבדוגמת המתגייסים היא ברורה למדי, אבל קשה מאד להיפטר ממנה כליל: אם נשתמש בנתוני קופות החולים, אולי נקבל ייצוג יתר של אוכלוסיית הקשישים; אם נדגום את באיו של מרכז־קניות כלשהו, אולי נחמיץ את בעלי ההכנסות הנמוכות במיוחד; וכו'.
דוגמא טובה לבעיית ההטיה היא "מיתוס עשרת האחוזים". הסקסולוג אלפרד קינסי (Kinsey) פרסם באמצע המאה העשרים את "דו"ח קינסי", והיכה בתדהמה את אמריקה השמרנית של התקופה כשטען, בין השאר, כי כעשרה אחוזים מהגברים האמריקאיים הם הומוסקסואלים. המדגם של קינסי היה מרשים בגודלו – כמה אלפי מרואיינים – אבל היה רחוק מלהיות מייצג; על מנת להקיף את שלל גוני המיניות האנושית, בחר קינסי לראיין מספר רב של הומוסקסואלים פעילים, שהיטו את התוצאה כלפי מעלה. למרות שמחקרים מאוחרים יותר הראו כי שיעור ההומוסקסואלים באוכלוסייה הוא קרוב לודאי נמוך משמעותית, "מיתוס עשרת האחוזים" קנה שביתה בקרב הציבור הרחב, והנתון (השגוי, כפי הנראה) מצוטט שוב ושוב גם כיום.
לענות בכנות או לשקר?
הדוגמא האחרונה ממחישה קושי נוסף בשלב איסוף הנתונים: לעתים קרובות מדידה ישירה של התופעה אותה הסטטיסטיקאי חוקר היא יקרה או אפילו בלתי אפשרית, ולכן הוא נאלץ להסתמך על עדותם של הנבדקים אודות עצמם. קל להבין מדוע חלק מהנבדקים יבחרו לשקר במקרים בהם הם סבורים שתשובה כנה תאיר אותם באור לא־מחמיא. לדוגמא, 95 אחוזים מהנשאלים בסקר טלפוני שנערך בארה"ב הצהירו כי הם נוהגים לשטוף את ידיהם לאחר ביקור בשירותים, אך מנתונים שנאספו על ידי משקיפים בבתי־שימוש ציבוריים עולה כי רק כ-67 אחוזים מהאמריקאים אכן עושים כך.
בעיית הדיווח השקרי מעיבה על מחקרים סטטיסטיים במגוון תחומים – חשבו למשל על העלמות מס, בגידות בחיי הנישואין או שימוש בסמים.
אפקט המגירה
אם נטיל מטבע הוגנת מאה פעמים, מספר הפעמים שהיא תיפול על "עץ" יהיה בסבירות גבוהה קרוב ל-50. סטייה משמעותית מ-50 (נניח, יותר מ-70 פעם) היא מאד לא סבירה, אבל עדיין אפשרית. לכן, אם נחזור על סדרת ההטלות מספר רב מאד של פעמים, לא יהיה זה מפתיע אם באחת מהסדרות נקבל "עץ" למעלה מ-70 פעם; צופה שייחשף רק לסדרה זו יהיה משוכנע, מן הסתם, שהמטבע אינה הוגנת.
דבר דומה מתרחש גם במחקרים אמיתיים. ניסויים מושפעים במידה כזו או אחרת ממזל אקראי טהור, שגם אם ניתן לצמצמו משמעותית (למשל על ידי הגדלת המדגם) לעולם לא ניתן לבטלו לחלוטין. לכן, אם מספר רב של חוקרים יבדקו בנפרד זה מזה את יעילותה של תרופה שלמעשה אינה עושה דבר, בהחלט ייתכן שאחד מהם "יגלה" שהתרופה חוללה פלאות בקרב מטופליו. אותו חוקר יזדרז לפרסם את ממצאיו, בעוד שעמיתיו המאוכזבים יעדיפו לגנוז את מחקריהם ה"כושלים".
תופעה זו – הקרויה "אפקט המגרה", על שם תחנתם האחרונה של המחקרים המאכזבים – מהווה בעיה רצינית במחקר המדעי כיום. פעמים רבות המחקרים ה"מוצלחים" (אך השגויים!) מתפרסמים על ידי חוקרים נקיי־כפיים, שערכו ביוזמתם ניסויים קפדניים ופעלו בתום לב, אך לא תמיד זהו המצב. אין זה נדיר שחברת־ענק תממן מספר רב של מחקרים בלתי־תלויים, אבל תפרסם את המחקר היחיד שתוצאותיו תואמות את האינטרסים שלה, תוך הדגשת העובדה שהוא נערך על ידי חוקרים עצמאיים, וללא כל התערבות מצידה.
מתאם וסיבתיות
במחקר דמיוני שנערך בקרב תלמידי כיתות ג'–ח' התגלתה תופעה מעניינת: התלמידים שכתבו עם מעט שגיאות כתיב, נטו להיות גבוהים יותר מחבריהם במידה משמעותית. נפתלי הוא תלמיד בכיתה ד', וחלום חייו הוא להיות כדורסלן; ביום בו שמע על המחקר, גמלה בליבו החלטה: הוא ישקוד על לימודיו, ילמד לאיית כהלכה, וכך ישיג עוד כמה סנטימטרים חשובים!
נפתלי נכשל בכשל מפורסם: מכך ש־א' קשור ל־ב' – ואפילו קשר הדוק – עדיין לא נובע כי א' הוא הסיבה ל־ב'. בדוגמא דנן, מיעוט שגיאות כתיב כמובן אינו גורם לגובה; מקור הקשר בין שני המשתנים הוא ששניהם מושפעים בצורה חזקה ביותר ממשתנה שלישי: הגיל. תלמידי הכיתות הגבוהות הם גם גבוהים יותר, וגם כותבים בפחות שגיאות, בהשוואה לתלמידי הכיתות הנמוכות.
ל"קשר" בין שני משתנים כגון "גובה" ו"שכיחות שגיאות כתיב" קוראים סטטיסטיקאים מתאם, וניתן למדוד את עוצמתו באופן מספרי. נפתלי נכשל בכך שלא הבדיל בין מתאם לבין סיבתיות. בדוגמא המלאכותית שלעיל הכשל הוא ברור ממבט ראשון, אך רבים וטובים נכשלים בו במקרים אחרים. למשל, המתאם הברור והמתועד היטב שבין עישון סיגריות לבין תחלואה בסרטן עדיין אינו מוכיח (עקרונית!) שהעישון גורם לסרטן; אין לפסול את האפשרות כי קיים דבר־מה הגורם לאנשים מסוימים גם לאהוב לעשן, וגם ללקות בסרטן.

(צילום: iStockPhoto)
גם כשבאמת קיים קשר סיבתי בין שני משתנים מתואמים, הוא לא תמיד בכוון המצופה. ילידי האיים ההיברידיים החדשים באוקיינוס השקט הבחינו במהלך הדורות כי לאנשים בריאים היו לעתים קרובות כינים, ואילו לחולים, כמעט תמיד לא; לכן, הם הסיקו, כינים מסייעות בשמירת הבריאות. הקשר האמיתי הוא בכוון ההפוך: כינים זקוקות לטמפרטורת גוף נורמלית כדי להתקיים, וכשזו עולה, הן עוזבות את ה"מארח" שלהן, ומחפשות אחר.
בקרה, פלצבו ועיוורון כפול
במטרה להבדיל בין מתאם לבין סיבתיות, עורכים חוקרים ניסויים מבוקרים. בניסויים כאלה, הנפוצים בתחום הרפואה, מחולקים משתתפי הניסוי לשתי קבוצות: חברי קבוצה אחת מקבלים טיפול כלשהו, בעוד חברי הקבוצה האחרת, הנקראת "קבוצת הביקורת", לא מקבלים את הטיפול. אם לטיפול יש אכן השפעה – דהיינו, אם קיימת סיבתיות – נצפה למצוא בתום הניסוי הבדלים ברורים בין שתי הקבוצות, שלא היו קיימים בתחילתו.
על מנת למנוע הטיות, חשוב לחלק את המשתתפים לשתי הקבוצות באופן אקראי. בניסוי לבדיקת יעילותו של כדור נגד מחלת־ים שנערך בשנות החמישים התקבלו תוצאות פנטסטיות: רוב חברי קבוצת הביקורת בהפלגת הניסוי חלו, בעוד שאלה שנטלו את הכדור חשו בטוב. בדיקה נוספת העלתה שרב־החובל, שהיה אחראי לחלק את הכדורים למשתתפים בניסוי, נתן אותם לצוות הספינה, והשתמש בנוסעים כקבוצת הביקורת. כלל לא ברור האם "הצלחת" הניסוי נבעה מפעולת הכדור, או שמא מההרכב השונה של שתי הקבוצות.
לא תמיד ניתן, טכנית או מוסרית, להורות לקבוצת אנשים לעשות דברים מסוימים – למשל, להתחיל לעשן או לעבור לגור בעיר אחרת. זוהי בעיה קשה, המעיבה על מחקרים סטטיסטיים רבים. בנוסף, כשהנבדקים הם בני־אנוש (ולא מכונות או צמחים, למשל), תוצאות המחקר עלולות להשתבש בשל תופעה פסיכו־פיסיולוגית מפורסמת הקרויה "אפקט הפלצבו": עצם הידיעה אודות קבלת טיפול עלולה להשפיע במידה משמעותית על מצב הנבדקים! לדוגמא, חולי אסטמה רבים מדווחים על שיפור במצבם, וכלי־הנשימה שלהם באמת מתרחבים, לאחר ששאפו חומר שתואר בפניהם כתרופה – גם אם למעשה אינו כזה.
בניסיון להתגבר על אפקט הפלצבו, נהוג לתת לחברי קבוצת הביקורת טיפול־דמה – לרוב "תרופה" שבעצם אין בה דבר – ולוודא שאיש ממשתתפי הניסוי לא יידע מי מטופל באמת ומי לא. במקרים רבים גם לרופאים המלווים את הנבדקים לא נאמר מיהם המטופלים האמיתיים, על מנת למנוע הטיות (מודעות או לא־מודעות) מצידם. שיטה זו, בה לא משתתפי הניסוי ולא הרופאים יודעים מיהם המטופלים האמיתיים, נקראת שיטת העיוורון הכפול. חוקרים קפדניים לא חוסכים במאמצים ליצירת עיוורון: בניסוי לבדיקת יעילותו של ניתוח חדשני (בזמנו) לטיפול במחלת לב מסוימת, הוכנסו משתתפי הניסוי לחדר הניתוח תחת הרדמה מלאה; רק לאחר שהמנתח ביצע את החיתוך המקדים הדרוש בבשרם הוא פתח מעטפה שהכילה הוראות האם להשלים את הניתוח או לא. לא החולים ולא רופאיהם האישיים ידעו מי נותח באופן מלא. הניתוח התגלה כחסר תועלת, לאחר שהסתבר כי מצבם של חברי קבוצת הביקורת השתפר במעט יותר מזה של חברי קבוצת הטיפול.
לא בכדי כתב הפיסיקאי רוברט פארק במאמר שבעה סימני אזהרה מפני מדע קלוקל: "התגלית החשובה ביותר של מדע הרפואה המודרני היא לא חיסונים או אנטיביוטיקה, אלא הניסוי האקראי בשיטת העיוורון הכפול, בזכותו אנו יודעים מה עובד ומה לא."
הממוצע המטעה
אילו היינו יכולים לבחור את טמפרטורת הסביבה האידיאלית, מה היא היתה? חלק נכבד מקוראי מאמר זה יסכים בודאי שטמפרטורה של כ-20 מעלות היא בחירה סבירה למדי. מה כל כך רע, אם כך, באקלים העיר ניו־יורק, בה הטמפרטורה הממוצעת במהלך היום היא 17 מעלות? הבעיה היא שהטמפרטורה בניו־יורק היא רק לעתים רחוקות 17 מעלות; החורף הניו־יורקי הוא קפוא והקיץ לוהט, ורק ממוצע הטמפרטורות על פני כל השנה יוצר אשליה של אקלים נוח.
הממוצע הוא ללא עוררין הגודל הסטטיסטי הנפוץ והמובן ביותר, אך כפי שממחישה הדוגמא האחרונה, הוא עלול להוליך שולל. חשוב מאוד לדעת, לפעמים, כיצד מפוזרים הנתונים סביב הממוצע. גודל סטטיסטי חשוב המודד עד כמה נרחב הוא פיזור זה נקרא "סטיית־תקן".
במקרים אחרים, יש לשים לב מאילו מספרים בדיוק מחושב הממוצע. תוחלת החיים באנגליה בתחילת המאה ה-19 היתה פחות משלושים שנה; מכאן, לכאורה, ניתן להסיק כי אלה שזכו להגיע לגיל 50 נחשבו לקשישים מופלגים, ששעתם קרובה. טעות! הסיבה המרכזית לתוחלת החיים הנמוכה היתה התמותה הגבוהה בקרב תינוקות וילדים צעירים – למעלה מארבעים אחוז מהאוכלוסייה נפטרו בטרם הגיעם לגיל 10. הנתון הרלוונטי לענייננו הוא אינו גיל הפטירה הממוצע בקרב כלל האוכלוסייה, אלא רק בקרב בני־המזל שזכו להגיע לגיל 50; האחרונים, מסתבר, נפטרו בממוצע בגיל 70 – גיל סביר גם בסטנדרטים של ימינו.
הצגת הנתונים
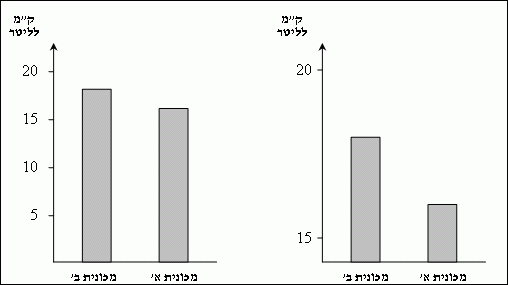
שני הגרפים הבאים משווים את צריכת הדלק של שתי מכוניות המתחרות על אותו פלח שוק. למרות ששניהם מכילים את אותו המידע בדיוק, הגרף הימני "מחמיא" למכונית ב' הרבה יותר. חידה (קלה): כיצד תבחר יצרנית מכונית ב' להציג את הנתונים בפרסומיה?
ניתן להשפיע על "השורה התחתונה" של מחקר גם באמצעות חלוקת תוצאותיו לקטגוריות בדרכים שונות. מהו גורם התמותה הראשון במעלה במדינת מורטליסטן? תלוי איך מגדירים "גורם". שתי טבלאות הנתונים שלהלן מסכימות זו עם זו, אך על פי הימנית, התשובה היא סרטן, ואילו על פי השמאלית, התשובה היא מחלות לב.

הסקה ופרשנות
מחקר שפורסם בעיתונות הפופולרית בתחילת שנות התשעים גילה כי כשני אחוזים מאזרחי ארה"ב הבוגרים נחטפו על ידי עב"מים. מהיכן הגיע מספר זה? על מנת לאפשר גם לחטופים שאינם מודעים לחטיפתם להצטרף לסטטיסטיקה, בחרו החוקרים שלא לשאול את הנבדקים על חטיפה באופן ישיר; במקום זאת, הם זיהו חמישה סימפטומים המאפיינים, לדעתם, חטיפות על ידי עב"מים (למשל: "להתעורר משותק תוך הרגשה כי בחדר נוכח אדם זר או משהו זר אחר"), והכריזו על כל מי שדיווח על ארבעה סימפטומים או יותר כנחטף.
זוהי דוגמא קיצונית לפרשנות מרחיקת־לכת של תוצאות מחקר. לעתים קרובות קיים קשר קלוש למדי בין תוצאותיו הגולמיות של מחקר לבין הכותרת לה הוא זוכה בעיתון, עקב נטייתם המוכרת של עורכי עיתונים לנסות לחולל סנסציות.
דוגמת החטיפות ממחישה גם את השרירותיות הטבועה לעתים בשלב הפרשנות. אילו היו החוקרים מסתפקים בשלושה סימפטומים לצורך סיווג הנבדקים כחטופים, השיעור המדווח היה בוודאי עולה משמעותית. בעיית "ההגדרה השרירותית" עולה שוב ושוב בפרשנות מחקרים: מתי, לדוגמא, נגדיר אדם כהומוסקסואל? האם די בהתנסות (או אפילו במחשבה) הומוסקסואלית אחת, או שרק פעילות בלעדית רבת־שנים הנמשכת עד הזמן האחרון תספיק? כל בחירה תשנה, כמובן, את כותרת הידיעה בעיתון.
אז מה לעשות?
כיצד ניתן, אם כן, להימנע מליפול במלכודות הסטטיסטיקה? להימנע לחלוטין כנראה שלא ניתן, אך אפשר לצמצם את מספר הנפילות ואת עומקן. עצה אחת היא לא להתעצל: מומלץ לקרוא באופן ביקורתי לא רק את כותרת הידיעה בעיתון, אלא גם את הניסוח המדויק של הכתבה. מה בדיוק גילה המחקר? כיצד נבחרו משתתפי הניסוי? האם הוא כלל קבוצת ביקורת? במקרים מסוימים, כדאי להתאמץ ולקרוא את המחקר המקורי, ואולי גם להשוות אותו עם מחקרים אחרים שנערכו בנושא. כלל פשוט וחשוב שיש לזכור הוא שמתאם אינו בהכרח מצביע על סיבתיות.
ספקנות, ואולי אף חשדנות, עשויות להועיל גם כן. מי מימן את המחקר? האם יש לו אינטרס בפרסום תוצאותיו? מהו המוניטין המדעי של החוקרים ושל כתב־העת בו המחקר התפרסם? נוכח מחקרים המתעדים תופעות על־טבעיות, ביקורי חוצנים, שיטות ריפוי פלאיות וכו', מומלץ לזכור את אמרתו המפורסמת של קרל סייגן, "טענות יוצאות מגדר הרגיל זקוקות להוכחות יוצאות מגדר הרגיל."
ולסיום, הולמות גם מילותיו של ה. ג'. וולס: "חשיבה סטטיסטית תהיה יום אחד חיונית עבור אזרחות טובה ממש כמו קריאה וכתיבה."
|
קישורים
אפקט הפלצבו - The Skeptic Dictionary
מתאמים מפוקפקים - דוגמאות המראות כיצד ניתן ליצור מתאמים מלאכותיים
|
|
 |






 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות




