ברשימה הקודמת סקרנו ברפרוף את המודל המתמטי של תורת הקוונטים. התורה, כפי שהתפתחה עד שנות השלושים, נותנת פרשנות מאוד מוגבלת למושגים המתמטיים והפיזיקליים – היא לא אומרת, למשל, דברים ברורים על מהותה של הסופרפוזיציה – אולי כי אין מה לומר.
פיזיקאים רבים לא היו מרוצים מהתורה. נראה שאחד היסודות בתורה שמפריעים להרבה פיזיקאים, עד היום אולי, הוא ממד האקראיות שבה. במודל שלנו, נכנסה האקראיות בשלב הקריסה: המערכת קרסה לאחד הערכים מתוך הסופרפוזיציה של פונקציית הגל, והערך ש"נבחר" נבחר, כך נראה, באקראי. הסיבה שנאמר שהוא נבחר באקראי לא היתה עקרונית: פשוט, בניסוי כמו ניסוי שטרן־גרלאך (הניסוי הבסיסי שהוצג בחלק א'), אם משגרים אלקטרון בודד, איננו יודעים על שום גורם שיקבע האם האלקטרון יסטה למעלה או למטה. אבל אפשר להעלות על הדעת שישנם גורמים שקובעים זאת באופן דטרמיניסטי, ופשוט איננו יודעים אותם עדיין. לגורמים כאלה קוראים "משתנים חבויים".
בין הפיזיקאים שהסתייגו מתורת הקוונטים בלט אלברט איינשטיין. מפורסמת קריאתו לנילס בור, מאבות תורת הקוונטים, "לא ייתכן שאלוהים משחק בקוביות!" (תשובתו של בור, אגב, היתה כנראה "הפסק לומר לאלוהים מה לעשות!"). כאתגר ממוקד יותר לתורת הקוונטים, כתב איינשטיין ב-1935, יחד עם הפיזיקאים בוריס פודולסקי ונתן רוזן, את המאמר "האם תיאור קוונטי של המציאות הפיזיקלית יכול להיחשב שלם?", ובו ניסוי מחשבה שמוביל למעין פרדוקס. מקובל לקרוא לניסוי (או למעין־פרדוקס) "EPR", על שם שלושת הוגיו.

אלברט איינשטיין (צילום: יוסף קארש)
EPR הבחינו שהמודל המתמטי של תורת הקוונטים אומר משהו מוזר, כאשר מדובר על מערכות הכוללות כמה חלקיקים. על פי המודל, כאשר מערכת כזו תקרוס היא תקרוס כולה – כל החלקיקים ישנו את מצבם. זאת, אפילו אם את המדידה, שהיא כזכור הגורמת לקריסה, אנו מבצעים רק על חלקיק אחד. מדידה שמבוצעת על חלקיק אחד משפיעה גם על חלקיק אחר, וההשפעה הזו מיידית ואינה תלויה בזמן ובמרחק. הניסוי שהם הציעו אוחז את השור הזה בקרניו. אנו נתאר וריאציה מסוימת על ניסוי זה, במונחים של ספינים שאנו מכירים מחלק א', שנוסחה לראשונה על־ידי דיוויד בוהם ב-1951.
בניסוי שלנו אנו לוקחים מקור של אלקטרונים – גוש חומר רדיואקטיבי מסוים, שפולט זוגות של אלקטרונים. שני האלקטרונים בכל זוג כזה נעים בכיוונים מנוגדים. נמדוד לשני האלקטרונים ספין-x, נניח. מה יקרה?
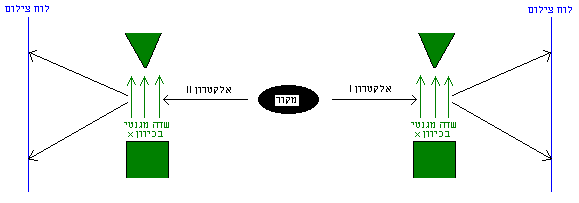
ניסוי 8
עדיין איננו יכולים לחזות מראש אם לאלקטרון I נמדוד ספין מעלה או מטה. אבל מתברר כי אם נמדוד לו ספין מעלה, אז גם לאלקטרון II נמדוד ספין מעלה; ולהפך. לשון אחר: אם נבצע מדידות רבות של זוגות, ונרשום את התוצאות כשתי סדרות של מספרים (סדרה אחת עבור האלקטרונים מצד ימין, והשנייה עבור צד שמאל), שתי הסדרות יראו אקראיות, אבל זהות. זאת, ללא תלות במרחק ביניהן: עד היום הצליחו לבצע ניסויים כאלו במרחקים של כמה מטרים. מדובר במרחק עצום, בקנה מידה של אלקטרונים, ובקושי טכנולוגי לא קטן, מכיוון שצריך, כזכור, לבודד היטב את מערכת הניסוי מהשפעות חיצוניות. עוד גורם שלא משנה כאן הוא סדר המדידות: נקבל את התוצאה הזו בין אם אנחנו מודדים צד אחד לפני הצד השני, או את שניהם בו־זמנית (עד כמה שאנו מסוגלים למדוד בו־זמניות).
כאשר EPR כתבו את מאמרם, לא ידעו עדיין לבצע ניסוי כזה; אבל זו כבר היתה התחזית של תורת הקוונטים. במודל של תורת הקוונטים, שני האלקטרונים הם מערכת אחת (בגלל אינטראקציה שהיתה ביניהם רגע לפני שהם יצאו מהמקור). אם אנו מודדים קודם בצד ימין, אז המדידה מקריסה את המערכת; אם היא קרסה לספין-x 'מעלה' (זה מה שמדדנו לאלקטרון בצד ימין), אז גם האלקטרון שבצד השמאלי קרס לספין-x 'מעלה', וזה מה שנמדוד לו אחר־כך. אם אנו חושבים שהמדידה היא בו־זמנית, אז מדובר במדידה אחת, עם תוצאה אחת.
מושג חשוב שעולה כאן הוא ה"צימוד" (entanglement), קשר בין שני אלקטרונים (או יותר), כך שהמצב שלהם הוא משותף, ומדידה של אחד מהם משפיעה על מדידות של השני. במאמר מוסגר נציין שהצימוד אינו בהכרח כזה שמצבם של שני האלקטרונים הוא סימטרי (כמו בניסוי שתיארנו) – על פי סוג המקור הרדיואקטיבי ייתכנו אפשרויות שונות של תלות. למעשה, מצב קוונטי אחד שנחקר רבות הוא "סינגלט" (Signlet): במצב זה שני האלקטרונים הם "הופכיים": אם לאחד מהם נמדוד ספין-x 'מעלה', לשני נמדוד בהכרח ספין-x 'מטה', וכך בכל כיוון של ספין. מכל מקום, לצד הסופרפוזיציה מהווה הצימוד את אחד המרכיבים שבהם נבדלת תורת הקוונטים באופן העמוק ביותר מהפיזיקה הקלאסית.
אבל כאן בא טיעון המחץ של EPR: הרי לא ייתכן שהמדידה בצד ימין משפיעה מרחוק על המדידה בצד שמאל! אם הניבוי של תורת הקוונטים נכון (ואנו יודעים כבר שהוא נכון), הרי שחייב להיות משהו באלקטרונים שקובע מראש את תוצאת המדידה. וזהו בדיוק משתנה חבוי. כלומר, תורת הקוונטים אינה שלמה. זהו המעין־פרדוקס שלהם, שבו תורת הקוונטים יורה לעצמה ברגל: אם היא נכונה, היא אינה שלמה. תורת הקוונטים אומרת שהאלקטרונים לפני המדידה הם בסופרפוזיציה של ערכי X, ושהמדידה גורמת להם באופן אקראי "לבחור" את אחד משני הערכים; אבל לא ייתכן שבחירה אקראית תהיה זהה בשני מקומות מרוחקים; הבחירה בעצם כבר טמונה באלקטרונים ברגע שבו הם יצאו מהמקור, והאקראיות היא רק למראית־עין, אומרים EPR. יש לנו עדיין עבודה קשה של חקירה וגילוי המשתנים החבויים הללו, באופן שישתלב עם הניסויים המוזרים שדנו בהם בחלק א'; אבל לפחות אפשר להתנחם בכך שהפיזיקה אינה אקראית, ואלוהים לא משחק בקוביות.
אי־שוויון בל
אם ניזכר בדברים בהם דנו בחלק א', נראה שההתאמה בין אלקטרונים בזוג אינה מוגבלת למצב בו מבצעים מדידה זהה (ספין-x). נניח שבצד ימין אנו מודדים ספין-x ובצד שמאל ספין-y. בחלק א' אמרנו שספין-x 'מעלה' הוא סופרפוזיציה של ספין-y 'מעלה' וספין-y 'מטה', במשקל חצי־חצי. מכאן, שאם בצד ימין מדדנו ספין-x 'מעלה', אזי בצד שמאל (שהאלקטרון בו נמצא במצב זהה לזה שבצד ימין) נמדוד ספין-y 'מעלה' ו'מטה' בסיכוי חצי־חצי. אותו דבר אם בצד ימין מדדנו ספין-x 'מטה'. מכאן ברור, שבסיכוי של חצי נקבל בשני הצדדים תוצאה זהה, ובסיכוי חצי – תוצאה שונה. נקבל זאת כתוצאה סטטיסטית, לאחר שנבדוק זוגות רבים.
אם נוסיף וניזכר במה שאמרנו בחלק א' על מדידות בזוויות שונות, אזי אם בשני הצדדים נמדוד ספינים בכיוונים שהפרשם 120 מעלות, נקבל ברבע מהזוגות תוצאה זהה, וב-3/4 מהזוגות תוצאה שונה. בעובדה זו נשתמש מיד, בעקבות ג'ון סטיוארט בל (Bell), כדי לטרוף מחדש את הקלפים בתמונת העולם הפיזיקלית.
במאמר משנת 1964, תחת הכותרת "על הפרדוקס של איינשטיין־פודלוסקי־רוזן", הציע בל ניסוי שהוא וריאציה על ניסויי EPR. על הניסוי שלו נעשו מאז וריאציות רבות, ואנו נתאר את זו שניסח מרמין (Mermin) ב-1981. שוב משגרים אלקטרונים לשני כיוונים, ומודדים עליהם ספין בשני הצדדים. אלא שכעת, כיוונו של השדה המגנטי אינו קבוע מראש. המכשיר שלנו בוחר, עבור כל אלקטרון, כיוון אחד מבין שלושה, והבחירה נעשית אקראית (ובסיכוי שווה) לאחר ששני האלקטרונים כבר יצאו מהמקור (אך כמובן, לפני שהגיעו למכשיר). שלושת הכיוונים האפשריים נבדלים זה מזה ב-120 מעלות. הבה נקרא להם B ,A ו-C.
מה יקרה אם שני המכשירים יבחרו באותו כיוון? נקבל בהכרח אותה תוצאה לשני האלקטרונים (שניהם מעלה, או שניהם מטה). מה יקרה אם המכשירים יבחרו כיוון שונה? נקבל ברבע מהזוגות תוצאה זהה, וב-3/4 מהזוגות תוצאה שונה. אלו הניבויים של תורת הקוונטים, שאושרו בניסויים (לפחות על אותן גרסאות של ניסוי בל שנוסו).
כעת ננסה לחשוב, איך אנו יכולים להסביר תוצאות כאלו בעזרת משתנים חבויים. הנחנו את קיומם כדי להסביר את ההתאמה של EPR (אותה התאמה שמתרחשת גם בניסוי הנוכחי, במקרים בהם הגרלנו את אותו כיוון בשני הצדדים). לשם כך, הנחנו ששני האלקטרונים יוצאים מהמקור כאשר הם כבר "יודעים" מהו הספין-x שלהם (כלומר, המשתנים החבויים כבר קובעים מראש את הערך). כעת עלינו להניח, באופן דומה, שהמשתנים החבויים קובעים מראש, בעת היציאה מהמקור, את ערכי הספין בכיוונים B ,A ו-C, בכל אחד משני האלקטרונים. ויתרה מכך, הערך שנקבע מראש לספין-A חייב להיות זהה עבור שני האלקטרונים (כי אם במקרה נמדוד לשניהם ספין-A, נקבל אותה תוצאה). הערך יכול להיות שונה מזוג לזוג (אנו יודעים שבחלק ממדידות ספין-A אנו מקבלים 'מעלה', ובחלק 'מטה') – אבל בזוג נתון, הוא בהכרח זהה לשני בני הזוג. באותו אופן, הערך שנקבע מראש לספין-B חייב להיות זהה, וכך גם לספין-C.
אבל כאשר האלקטרונים יוצאים מהמקור (והערך לכל מדידת ספין כבר נקבע), עדיין לא קבענו איזה ספין נמדוד לכל אחד מהם – זה מוגרל רק לאחר היציאה. לכן, אם נניח שלשני האלקטרונים בזוג מסוים נקבע מראש ספין-A 'מעלה', ובצד ימין למשל אנו אכן מודדים ספין-A, התוצאה חייבת להיות מעלה, ללא תלות בכיוון שבחרנו למדוד לאלקטרון שמאל.
אם כן, ברגע שזוג אלקטרונים יוצא מהמקור, בהכרח קבועים לשני האלקטרונים ערכי הספין שימדדו בכל שלושת הכיוונים, ויש לנו שמונה אפשרויות:
(ספין-A, ספין-B, ספין-C)
1. מעלה־מעלה־מעלה
2. מעלה־מעלה־מטה
3. מעלה־מטה־מעלה
4. מעלה־מטה־מטה
5. מטה־מעלה־מעלה
6. מטה־מעלה־מטה
7. מטה־מטה־מעלה
8. מטה־מטה־מטה
איננו יודעים, עבור כל זוג נתון, באיזו אפשרות הוא "בחר", ולא בהכרח הסיכוי לשמונת הצירופים הוא שווה. נבדוק, בכל זאת, מה אנו יכולים לומר על הסיכוי לתוצאה זהה ('מעלה' בשני הצדדים או 'מטה' בשניהם), באותם זוגות שבהם מדדנו ספין בכיוונים שונים.
נניח שזוג מסוים "בחר" באפשרות 2. אם נמדוד לו בצד אחד ספין-A, ובצד השני ספין-B, נקבל תוצאה זהה ('מעלה'). אם נמדוד A ו-C, או B ו-C, נקבל תוצאה שונה. מכיוון ששלושת הצירופים נמדדים בסיכוי שווה, אנו מקבלים שעבור זוגות כאלה, בשליש מהמדידות שונות־הכיוון נקבל תוצאה זהה. באותו אופן, נקבל תוצאה זהה בשליש מהמדידות שונות־הכיוון עבור זוגות ש"בחרו" באפשרויות 3 עד 7 (שני כיוונים זהים ואחד שונה).
מה עם זוגות ש"בחרו" באפשרות 1 או 8 (שלושה כיוונים זהים)? בהם בהכרח נקבל תוצאה זהה בשני הצדדים. נובע מכך שבכל "בחירה", ההסתברות לתוצאה זהה היא או שליש או אחד. ומכאן ברור שבסך הכל (בלי לדעת שום דבר על ההסתברות לבחירה בצירוף כזה או אחר מבין השמונה), ההסתברות לתוצאה זהה היא לפחות שליש.
לעומת זאת, בניסוי (ועל־פי תורת הקוונטים), הסיכוי לתוצאה זהה במדידה שונת־כיוון הוא כזכור רבע. זהו "אי־שוויון בל". ההפרש בין שני הצדדים הוא מספיק גדול כדי לשלול הסבר ע"י טעות בניסוי. עוד לפני שמצאנו תורה של משתנים חבויים שתסביר לנו את ניסוי EPR, אנו כבר יודעים שאין טעם לחפש.
מעניין לציין כי אי־השוויון מתקיים כאן רק ברמה הסטטיסטית: אין לנו מדידה אחת שתוצאתה אינה מתיישבת עם משתנים חבויים; רק מדידות רבות ישכנעו אותנו בכך. ישנה גרסה של ניסוי בל מ-1989, שנקראת GHZ (גרינברגר, הורן, זיילינגר); בגרסה זו משתמשים בשלישייה של אלקטרונים במקום בזוג, ומודדים ספין-x או ספין-y. בניסוי זה, הכישלון של משתנים חבויים אינו סטטיסטי אלא מתקיים בכל מדידה ומדידה: התוצאות בכל שלישייה מקיימות תכונה מסוימת, על פי תורת הקוונטים, תכונה שמשתנים חבויים לא יכולים לקיים אותה. הבעיה היא שעדיין איננו יודעים לבצע את GHZ במעבדה.
לאחר שויתרנו על משתנים חבויים, עלינו לחזור אחורה ולבדוק שוב את הטיעון של EPR, שבעקבותיו הסקנו שבהכרח יש משתנים חבויים. אולי מדידה אחת כן משפיעה על המדידה השנייה מרחוק? אבל נראה שכדי להסביר השפעה כזו, בדרכים פיזיקליות מקובלות, עלינו להניח שמשהו פיזיקלי עובר בין שתי המדידות: תנועה של חלקיקים, זרימה של אנרגיה, התפשטות במרחב של כוח או שדה. לא ידוע לנו על כל מעבר כזה, ויתרה מכך: כל התפשטות או תנועה שכזו מוגבלת במהירותה – כך לימדה אותנו תורת היחסות, שקבעה את מהירות האור כגבול עליון לתהליכים כאלו. ואילו כאן אנו יכולים לבצע את שתי המדידות בו־זמנית. ואפילו אם קשה לדבר על "בו־זמניות" אמיתית, לכל הפחות אנו יודעים להבטיח מרווח זמן קטן – כה קטן, עד שלא ייתכן שמשהו עבר בין שני המכשירים במרווח זמן זה, אפילו במהירות האור.
אולי נוותר על תורת היחסות? זה יהיה עצוב, שכן מדובר בתיאוריה מבוססת היטב תיאורטית ונסיונית. העיקרון שלכאורה מופר בניסוי בל אינו תוצאה משנית של תורת היחסות, אלא אחד מאבני היסוד שלה. ממילא, גם אם היינו מוותרים על תורת היחסות, אין לנו עדיין תיאוריה שתסביר לנו בפירוט כיצד מתרחשת ההשפעה המופלאה בין המדידות.
אז אולי אין כאן השפעה של מדידה אחת על מדידה אחרת, אלא שתיהן הן, במובן יסודי ועמוק, חלק ממערכת אחת? זוהי התמונה המצטיירת במודל של תורת הקוונטים. לאחר שהתורה ביקשה מאתנו לקבל את הסופרפוזיציה, אנו מתבקשים כעת לעכל מושג קשה נוסף: "אי־לוקאליות". המערכת הקוונטית מתנהגת כיחידה אחת, גם כאשר היא כוללת רכיבים מרוחקים זה מזה במרחב.
לפני שאנו מזדעזעים, יש לציין כי הלוקאליות לא היתה תמיד ערך חשוב בפיזיקה. למעשה, הפיזיקה הניוטונית, זו שלמדנו בבית־הספר, לא היתה לוקאלית: אם השמש נעה מנקודה א' לנקודה ב', השפעת התנועה על כדור הארץ, מבחינת כוח הכבידה, היא מיידית. אמנם ככל שגדל המרחק מהשמש ההשפעה חלשה יותר, אולם שינויים מתרחשים מיידית בכל המרחב. רק תורת היחסות הכללית הכניסה לפיזיקה את הטענה שהשפעות כאלו מתקדמות במהירות מסוימת (לכל היותר, מהירות האור), ולכן ניתן לדבר על לוקאליות: אירוע שמתרחש בנקודה א' ישפיע על נקודה ב' רק באמצעות תיווך, שעובר בין נקודות רצופות. יש בכך משהו שקוסם לאינטואיציה (ושוב, חיזוקים תיאורטיים ונסיוניים שבגללם תורת היחסות נחשבת למוצלחת כל כך); את זה עלינו ליישב איכשהו עם התוצאות של העולם הקוונטי.
עד עתה אנו יכולים לומר שכל הבעיות הן רק באינטואיציה הקלוקלת שלנו – שמתעקשת לדבוק במושגים מפוקפקים כמו לוקאליות, או מיקום מדויק במרחב (בניגוד לסופרפוזיציה) – ותורת הקוונטים עצמה היא בסדר. עובדה, הניבויים שלה עובדים מצוין, ודווקא כאשר הם סותרים את האינטואיציה. אלא שיש בתורת הקוונטים גם בעיה פנימית, אפשר לומר – סתירה. זוהי "בעיית המדידה". בחלק הבא נציג אותה, ונציג גם שני נסיונות תיאורטיים לפתור אותה: של ויגנר ושל GRW. בחלק האחרון נדון בפתרון של בוהם, ובפתרונות ממשפחת "תיאוריית העולמות המרובים".
|
קישורים
ברשימה הקודמת חלק א' של המאמר
|






 RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות
RSS מאמרים |
כתבו למערכת |
אודות האתר |
טרם התעדכנת |
ארכיון |
חיפוש |
עזרה |
תנאי שימוש והצהרת נגישות


